
分析 (1)分别求出语、数、英、综合四门学科安排在上午第一场考试的排法,再求出其它7课的排法,相乘即可;
(2)求出数学、化学在第四天上午的方法,再求出安排前3天同一天考试的方法,从而求出满足条件的概率即可.
解答 解:(1)若语、数、英、综合四门学科安排在上午第一场考试共有:${A}_{4}^{4}$种排法,
其它7课共有${A}_{7}^{7}$种排法,
由${A}_{4}^{4}$×${A}_{7}^{7}$=120960,
得:考试日程安排表有120960种不同的安排方法;
(2)数学、化学在第四天上午共有${A}_{2}^{2}$×${A}_{9}^{9}$种方法,
安排前3天同一天考共有:${C}_{3}^{1}$×${A}_{3}^{2}$×${A}_{9}^{9}$种方法,
故所求的概率P=$\frac{{A}_{2}^{2}{×A}_{9}^{9}{+C}_{3}^{1}{×A}_{3}^{2}{×A}_{9}^{9}}{{A}_{11}^{11}}$=$\frac{2+3×3×2}{11×10}$=$\frac{2}{11}$.
点评 本题考查了列举法求条件概率的问题,考查排列组合问题,是一道基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
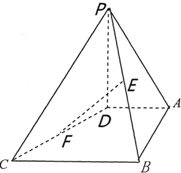 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=5,PD=8,点E,F分别是PB,DC的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=5,PD=8,点E,F分别是PB,DC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
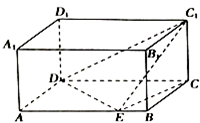 如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2,E是线段AB上的点,且EB=1,则二面角C-DE-C1的正切值为$\frac{\sqrt{2}}{2}$.
如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2,E是线段AB上的点,且EB=1,则二面角C-DE-C1的正切值为$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
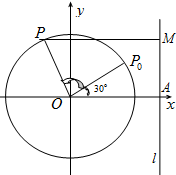 如图,圆O的半径为2,l为圆O外一条直线,圆心O到直线l的距离|OA|=3,P0为圆周上一点,且∠AOP0=$\frac{π}{6}$,点P从P0处开始以2秒一周的速度绕点O在圆周上按逆时针方向作匀速圆周运动.t秒钟后,点P到直线l的距离用t(t≥0)可以表示为3-2cos(πt+$\frac{π}{6}$),t≥0.
如图,圆O的半径为2,l为圆O外一条直线,圆心O到直线l的距离|OA|=3,P0为圆周上一点,且∠AOP0=$\frac{π}{6}$,点P从P0处开始以2秒一周的速度绕点O在圆周上按逆时针方向作匀速圆周运动.t秒钟后,点P到直线l的距离用t(t≥0)可以表示为3-2cos(πt+$\frac{π}{6}$),t≥0.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5$\sqrt{3}$ | B. | 5 | C. | -5$\sqrt{3}$ | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com