
分析 根据f(x)的解析式结合正弦函数的周期性,得出f(x)的图象关于x=3对称,从而得出F((x)的对称性,作出函数的图象即可得m的取值范围.
解答  解:sin$[\frac{π}{6}(6-x)]$=sin($π-\frac{π}{6}x)$=sin$\frac{π}{6}x$
解:sin$[\frac{π}{6}(6-x)]$=sin($π-\frac{π}{6}x)$=sin$\frac{π}{6}x$
∴f(6-x)=f(x),
f(x)的图象关于x=3对称,
g(6-x)=g(x),
∴g(x)的图象关于x=3对称,
∴F(x)=f(x)+g(x)的图象关于x=3对称,即F(6-x)=F(x),
F(a2+a-1)=F(2a-m),
∴a2+a-1=2a-m或a2+a-1=6-(2a-m)
∴m=-a2+a+1或m=a2+3a-7,
要使方程有四个不等是跟,m的取值需要在C点以下,F点以上,且不包括:A(-$\frac{1+\sqrt{17}}{2},-4-\sqrt{17})$,B($\frac{-1+\sqrt{17}}{2},\sqrt{17}-4)$处的函数值,
故m的取值范围是(-$\frac{37}{4},-4-\sqrt{17})$$∪(-4-\sqrt{17},\sqrt{17}-4)∪(\sqrt{17}-4$,$\frac{5}{4})$.
点评 本题主要考查函数的图象和性质,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届云南曲靖市高三上半月考一数学试卷(解析版) 题型:选择题
在区间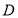 上,若函数
上,若函数 为增函数,而函数
为增函数,而函数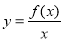 为减函数,则称函数
为减函数,则称函数 为区间
为区间 上的“弱增”函数.则下列函数中,在区间
上的“弱增”函数.则下列函数中,在区间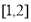 上不是“弱增”函数的为( )
上不是“弱增”函数的为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?F∈BC,EF⊥AD | B. | ?F∈BC,EF⊥AC | C. | ?F∈BC,EF≥$\sqrt{3}$ | D. | ?F∈BC,EF∥AC |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com