
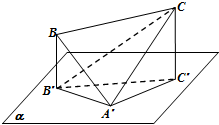
 如图,已知边长为2的正△A′BC,顶点A′在平面α内,顶点B,C在平面α外的同一侧,点B′,C′分别为B,C在平面α上的投影,设|BB′|≤|CC′|,直线CB′与平面A′CC′所成的角为φ.若△A′B′C′是以∠A′为直角的直角三角形,则tanφ的范围为$[{\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2}})$.
如图,已知边长为2的正△A′BC,顶点A′在平面α内,顶点B,C在平面α外的同一侧,点B′,C′分别为B,C在平面α上的投影,设|BB′|≤|CC′|,直线CB′与平面A′CC′所成的角为φ.若△A′B′C′是以∠A′为直角的直角三角形,则tanφ的范围为$[{\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2}})$. 分析 由题意找出线面角,设BB′=a,CC′=b,可得ab=2,然后由a的变化得到A′B′的变化范围,从而求得tanφ的范围.
解答 解:如图, 由CC′⊥α,A′B′?α,得A′B′⊥CC′,
由CC′⊥α,A′B′?α,得A′B′⊥CC′,
又A′B′⊥A′C′,且A′C′∩CC′=C′,
∴A′B′⊥面A′C′C,则φ=∠B′CA′,
设BB′=a,CC′=b,则A′B′2=4-a2,A′C′2=4-b2,
设B′C′=c,
则有$\left\{\begin{array}{l}{4-{a}^{2}+4-{b}^{2}={c}^{2}}\\{(\frac{c}{2})^{2}+(\frac{a+b}{2})^{2}=3}\end{array}\right.$,整理得:ab=2.
∵|BB′|≤|CC′|,∴a≤b,
tanφ=$\frac{A′B′}{2}$,
在三角形BB′A′中,∵斜边A′B为定值2,
∴当a最大为$\sqrt{2}$时,A′B′取最小值$\sqrt{2}$,tanφ的最小值为$\frac{\sqrt{2}}{2}$.
当a减小时,tanφ增大,
若a≤1,则b≥2,在Rt△A′CC′中出现直角边大于等于斜边,矛盾,
∴a>1,此时A′B′<$\sqrt{3}$,即tanφ$<\frac{\sqrt{3}}{2}$.
∴tanφ的范围为$[{\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2}})$.
故答案为:$[{\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2}})$.
点评 本题考查了直线与平面所成的角,考查了空间想象能力和思维能力,灵活性强,属有一定难度题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
 将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=$\sqrt{2}$.
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知正△PAB和菱形ABCD,面PAB⊥面ABCD,∠BAD=60°.
已知正△PAB和菱形ABCD,面PAB⊥面ABCD,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在三棱锥P-ABC中,AC=BC=AP=BP=$\sqrt{2}$,PC=$\sqrt{3}$,AB=2.
在三棱锥P-ABC中,AC=BC=AP=BP=$\sqrt{2}$,PC=$\sqrt{3}$,AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com