
分析 (1)根据题意,满足x2+y2-4x+1=0的点P(x,y)在以C(2,0)为圆心,半径为$\sqrt{3}$的圆上,而x2+y2=|OP|2.因此当P、O、C三点共线时,|OP|达到最大值或最小值.由此结合点到直线的距离公式,即可求出x2+y2的最大值和最小值;
(2)由$\left\{\begin{array}{l}{y=k(x+1)}\\{{(x-2)}^{2}{+y}^{2}=3}\end{array}\right.$得:(1+k2)x2+(2k2-4)x+k2+1=0,根据△=(2k2-4)2-4(k2+1)2=0,从而求出$\frac{y}{x+1}$的最值.
解答 解:(1)∵实数x,y满足x2+y2-4x+1=0,可化成(x-2)2+y2=3
∴满足x2+y2-4x+1=0的点P(x,y)在以C(2,0)为圆心,半径为$\sqrt{3}$的圆上
而x2+y2=|OP|2,
∵当P、O、C三点共线时,|OP|达到最大值或最小值
∴当圆C上的点P在OC延长线上时,|OP|的最大值为|OC|+$\sqrt{3}$=2+$\sqrt{3}$.
得到x2+y2的最大值为(2+$\sqrt{3}$)2=7+4$\sqrt{3}$;
当圆C上的点P在线段OC上时,|OP|的最小值为|OC|-$\sqrt{3}$=2-$\sqrt{3}$,
得到x2+y2的最小值为(2-)2=7-4$\sqrt{3}$.
综上所述,x2+y2的最大值为7+4$\sqrt{3}$;最小值为7-4$\sqrt{3}$;
(2)满足x2+y2-4x+1=0的点(x,y)在以C(2,0)为圆心,半径为$\sqrt{3}$的圆面上,
$\frac{y}{x+1}$表示过圆面上的点和点(-1,0)的直线的斜率,
设过(-1,0)的直线方程是:y=k(x+1),
由$\left\{\begin{array}{l}{y=k(x+1)}\\{{(x-2)}^{2}{+y}^{2}=3}\end{array}\right.$得:(1+k2)x2+(2k2-4)x+k2+1=0,
由△=(2k2-4)2-4(k2+1)2=0,解得:k=±$\frac{\sqrt{2}}{2}$,
∴${(\frac{y}{x+1})}_{min}$=-$\frac{\sqrt{2}}{2}$,${(\frac{y}{x+1})}_{max}$=$\frac{\sqrt{2}}{2}$.
点评 本题给出满足二次方程的实数x、y,求x2+y2和$\frac{y}{x+1}$的最值,着重考查了圆的标准方程、点到直线的距离公式和二元函数最值的求法以及直线的斜率等知识,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 如图,直棱柱ABC-A1B1C1的底面△ABC中,CA=CB=1,∠ACB=90°,棱AA1=2,如图,以C为原点,分别以CA,CB,CC1为x,y,z轴建立空间直角坐标系
如图,直棱柱ABC-A1B1C1的底面△ABC中,CA=CB=1,∠ACB=90°,棱AA1=2,如图,以C为原点,分别以CA,CB,CC1为x,y,z轴建立空间直角坐标系查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
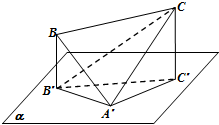 如图,已知边长为2的正△A′BC,顶点A′在平面α内,顶点B,C在平面α外的同一侧,点B′,C′分别为B,C在平面α上的投影,设|BB′|≤|CC′|,直线CB′与平面A′CC′所成的角为φ.若△A′B′C′是以∠A′为直角的直角三角形,则tanφ的范围为$[{\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2}})$.
如图,已知边长为2的正△A′BC,顶点A′在平面α内,顶点B,C在平面α外的同一侧,点B′,C′分别为B,C在平面α上的投影,设|BB′|≤|CC′|,直线CB′与平面A′CC′所成的角为φ.若△A′B′C′是以∠A′为直角的直角三角形,则tanφ的范围为$[{\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2}})$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com