
某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共100个,生产一个卫兵需5min,生产一个骑兵需7min,生产一个伞兵需4min,已知总生产时间不超过10h.若生产一个卫兵可获利润5元,生产一个骑兵可获利润6元,生产一个伞兵可获利润3元.
(1)用每天生产的卫兵个数x与骑兵个数y表示每天的利润W(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
设变量x、y满足约束条件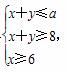 且不等式x+2y≤14恒成立,则实数a的取值范围是( )
且不等式x+2y≤14恒成立,则实数a的取值范围是( )
A.[8,10] B.[8,9] C.[6,9] D.[6,10]
查看答案和解析>>
科目:高中数学 来源: 题型:
若实数x,y满足x|x|-y|y|=1,则点(x,y)到直线y=x的距离的取值范围是( )
A.[1, ) B.(0,
) B.(0, ]
]
C.(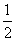 ,1) D.(0,1]
,1) D.(0,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
如果f ′(x)是二次函数,且f ′(x)的图象开口向上,顶点坐标为(1,-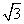 ),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是________.
),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com