
| ������ | 70 | 110 | 140 | 160 | 200 | 220 |
| Ƶ�� | $\frac{1}{20}$ | $\frac{4}{20}$ | $\frac{2}{20}$ |
| A�� | 0.4 | B�� | 0.3 | C�� | 0.2 | D�� | 0.1 |
���� �������20�����·ݽ�����Ƶ�ʷֲ������ɴ�������������·ݸ�ˮ������վ�ķ���������490����ǧ��ʱ����530����ǧ��ʱ���ĸ��ʣ�
��� �⣺�����������У�������Ϊ110������3����Ϊ160������7����Ϊ200������3����
�ʽ�20�����·ݽ�����Ƶ�ʷֲ���Ϊ��
| ������ | 70 | 110 | 140 | 160 | 200 | 220 |
| Ƶ�� | $\frac{1}{20}$ | $\frac{3}{20}$ | $\frac{4}{20}$ | $\frac{7}{20}$ | $\frac{3}{20}$ | $\frac{2}{20}$ |
���� ���⿼����ʵ����ǻ����⣬����ʱҪ�������⣬ע�⻥���¼����ʼӷ���ʽ�ĺ������ã�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
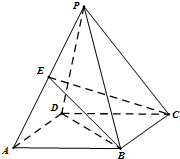 ��ͼ������P-ABCD�ĵ���ABCD�DZ߳�Ϊ2�����Σ���BCD=60�㣬��֪PB=PD=2��$PA=\sqrt{6}$��
��ͼ������P-ABCD�ĵ���ABCD�DZ߳�Ϊ2�����Σ���BCD=60�㣬��֪PB=PD=2��$PA=\sqrt{6}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���Ӳ�Ʒ | ���� | �ܼ� | |
| ���� | 16 | 8 | 24 |
| �� | 6 | 12 | 18 |
| �ܼ� | 22 | 20 | 42 |
| P��K2��k0�� | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
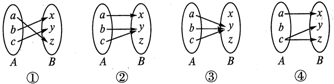
| A�� | �٢ڢ� | B�� | �٢ۢ� | C�� | �٢ڢ� | D�� | �ڢۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com