
分析 根据题意,设g(x)=f(x)+x,由函数的奇偶性的性质分析可得函数g(x)为R上的奇函数,又由有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}>-1$分析可得$\frac{g({x}_{1})-g({x}_{2})}{{x}_{1}-{x}_{2}}$>0,即可得函数g(x)=f(x)+x在区间(0,+∞)为增函数,结合函数的奇偶性可得g(x)在(-∞,0)为增函数;进而分析可得g(-2)=-3,g(0)=0,则等式-3≤f(x)+x≤0可以转化为g(-2)≤g(x)≤g(0),结合函数的单调性分析可得答案.
解答 解:根据题意,设g(x)=f(x)+x,
又由函数f(x)是定义在R上的奇函数,则有f(-x)=-f(x),
则有g(-x)=f(-x)+(-x)=-f(x)-x=-[f(x)+x]=-g(x),即函数g(x)为R上的奇函数,
则有g(0)=0;
又由对任意0<x1<x2,有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}>-1$,
即$\frac{[f({x}_{1})+{x}_{1}]-[f({x}_{2})+{x}_{2}]}{{x}_{1}-{x}_{2}}$=$\frac{g({x}_{1})-g({x}_{2})}{{x}_{1}-{x}_{2}}$>0,
则函数g(x)=f(x)+x在区间(0,+∞)为增函数,
又由函数g(x)为R上的奇函数,则g(x)在(-∞,0)为增函数,
又由f(2)=1,则f(-2)=-1,g(-2)=f(-2)+(-2)=-3;
不等式-3≤f(x)+x≤0?g(-2)≤g(x)≤g(0),
则有-2≤x≤0,
即不等式-3≤f(x)+x≤0的解集为[-2,0];
故答案为:[-2,0].
点评 本题考查函数的奇偶性与单调性的综合应用,关键是构造函数g(x),利用特殊值转化分析不等式.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | 4 | C. | $\frac{1}{9}$log32 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2+1≥0 | B. | ?x0∈R,x${\;}_{0}^{2}$+1>0 | ||
| C. | ?x∈R,x2+1>0 | D. | ?x0∈R,x${\;}_{0}^{2}$+1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>b>a | B. | b>a>c | C. | a>b>c | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源:2017届山西临汾一中高三10月月考数学(理)试卷(解析版) 题型:解答题
已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,椭圆
,椭圆 过点
过点 ,直线
,直线 交
交 轴于
轴于 ,且
,且 ,
,  为坐标原点.
为坐标原点.
(1)求椭圆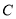 的方程;
的方程;
(2)设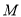 是椭圆
是椭圆 的上顶点,过点
的上顶点,过点 分别作直线
分别作直线 交椭圆
交椭圆 于
于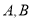 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为 ,且
,且 ,证明:直线
,证明:直线 过定点.
过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com