在等差数列{an}中，若an>0，公差d>0，则有a4·a6>a3·a7，类比上述性质，在等比数列{bn}中，若bn>0，q>1，则下列有关b4，b5，b7，b8的不等关系
正确的是________．
①b4＋b8>b5＋b7；②b5＋b7>b4＋b8；③b4＋b7>b5＋b8；④b4＋b5>b7＋b8.
科目：高中数学 来源： 题型：
某家电产品受在保修期内维修费等因素的影响，企业生产每件的利润与该产品首次出现故障的时间有关．某厂家生产甲、乙两种品牌，保修期均为2年．现从该厂已售出的两种品牌家电中各随机抽取50件，统计数据如下：
| 品牌 | 甲 | 乙 | |||
| 首次出现故障时间x(年) | 0<x≤1 | 1<x≤2 | x>2 | 0<x≤2 | x>2 |
| 数量(件) | 2 | 3 | 45 | 5 | 45 |
| 每件利润(百元) | 1 | 2 | 3 | 1.8 | 2.9 |
将频率视为概率，解答下列问题：
(I)从该厂生产的甲、乙品牌产品中随机各抽取一件，求其至少有一件首次出现故障发生在保修期内的概率；
(II)若该厂生产的家电均能售出，记生产一件甲品牌的利润为X1，生产一件乙品牌家电的利润为X2，分别求X1，X2的分布列；
(III)该厂预计今后这两种品牌家电销量相当，由于资金限制，只能生产其中一种品牌的家电．若从经济效益的角度考虑，你认为应生产哪种品牌的家电？说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知抛物线y2＝2px(p>0)，过定点(p,0)作两条互相垂直的直线l1、l2，若l1与抛物线交于
P、Q两点，l2与抛物线交于M、N两点，l1的斜率为k，某同学已正确求得弦PQ的中点坐标为(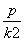
＋p，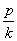
)，请你写出弦MN的中点坐标：________.
查看答案和解析>>
科目：高中数学 来源： 题型：
已知数列{an}的前n项和为Sn，且Sn＝n2＋1.则此数列的前4项分别为a1＝______，a2＝________，a3＝________，a4＝________.据此猜测，数列{an}的通项公式为an＝
____________________________________________
___________________________.
查看答案和解析>>
科目：高中数学 来源： 题型：
命题“若x2＜1，则－1＜x＜1”的逆否命题是______．(填序号)
①若x2≥1，则x≥1或x≤－1；
②若－1＜x＜1，则x2＜1；
③若x＞1或x＜－1，则x2＞1
；
④若x≥1或x≤－1，则x2≥1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
.(你能用几种方法证明？)
.
”的推理过程中，其大前提是______________．