练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知抛物线y2＝2px(p>0)，过定点(p,0)作两条互相垂直的直线l1、l2，若l1与抛物线交于

    P、Q两点，l2与抛物线交于M、N两点，l1的斜率为k，某同学已正确求得弦PQ的中点坐标为(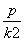＋p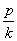，)，请你写出弦MN的中点坐标：________.


     (pk2＋p，－pk)


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在直角坐标系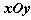中，以原点O为极点，x轴的正半轴为极轴，建立极坐标系.

    已知曲线C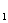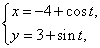： （t为参数）， C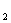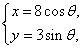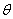：（为参数）。

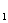    （I）化C，C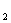的方程为普通方程，并说明它们分别表示什么曲线；

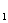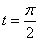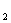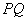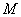    （II）若C上的点P对应的参数为，Q为C上的动点，求中点到直线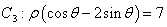  距离的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    数列－3,7，－11,15，…的通项公式是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若下列两个方程x2＋(a－1)x＋a2＝0，x2＋2ax－2a＝0中至少有一个方程有实根，则实数a的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在等差数列{an}中，若an>0，公差d>0，则有a4·a6>a3·a7，类比上述性质，在等比数列{bn}中，若bn>0，q>1，则下列有关b4，b5，b7，b8的不等关系正确的是________．

    ①b4＋b8>b5＋b7；②b5＋b7>b4＋b8；③b4＋b7>b5＋b8；④b4＋b5>b7＋b8.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    有两种花色的正六边形地板砖，按下面的规律拼成若干个图案，则第6个图案中有底纹的正六边形的个数是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设M是具有以下性质的函数f(x)的全体：对于任意s>0，t>0，都有f(s)＋f(t)<f(s＋t)．给出函数f1(x)＝log2x，f2(x)＝2x－1.下列判断正确的是________．

    ①f1(x)∈M；②f1(x)∉M；

    ③f2(x)∈M；④f2(x)∉M.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    由1＝12,1＋3＝22,1＋3＋5＝32,1＋3＋5＋7＝42，…，得到1＋3＋…＋(2n－1)＝n2用的是________推理．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设A、B为两个集合，下列四个命题：

    ①A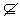B⇔对任意x∈A，有x∉B；②A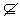B⇔A∩B＝∅；③A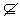B⇔A⊉B；④A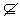B⇔存在x∈A，使得x∉B.

    其中真命题的序号是________(把符合要求的命题的序号都填上)．

    查看答案和解析>>

    同步练习册答案