练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图所示，球面上有四个点P、A、B、C，如果PA，PB，PC两两互相垂直，且PA=PB=PC=a，该球的表面积是
     
    ．
    考点：球的体积和表面积
    专题：计算题,空间位置关系与距离
    分析：PA、PB、PC可看作是正方体的一个顶点发出的三条棱，所以过空间四个点P、A、B、C的球面即为棱长为a的正方体的外接球，球的直径即是正方体的对角线，求出对角线长，即可求出球的表面积．
    解答： 解：空间四个点P、A、B、C在同一球面上，PA、PB、PC两两垂直，且PA=PB=PC=a，
    则PA、PB、PC可看作是正方体的一个顶点发出的三条棱，
    所以过空间四个点P、A、B、C的球面即为棱长为a的正方体的外接球，球的直径即是正方体的对角线，长为
    		3
    a，所以这个球面的面积S=4π(
    		3
    2
    a)2    =3πa2．
    故答案为：3πa2．
    点评：本题是基础题，考查球的内接体知识，球的表面积的求法，考查空间想象能力，计算能力，分析出，正方体的对角线就是球的直径是解好本题的关键所在．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    人民日报3月14日报道，中国人民银行已下发通知，要求暂停二维码（条码）支付，虚拟信用卡等支付业务和产品．前不久，某调研机构调研了在校大学生网上购物的情况，随机调查了16位在校大学生的网购比例，结果如茎叶图所示（图中茎7叶3表示73%，其余相同）：
    （Ⅰ）求从这16个在校大学生随机选取3个，至多有1个网购比例不低于95%的概率；
    （Ⅱ）以这16个在校大学生的样本数据来估计全国的总体数据，若从全国任选3位大学生，记ξ表示抽到网购比例不低于95%的人数，求ξ的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

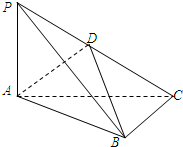    在三棱锥P-ABC中，PA⊥平面ABC，AP=AB=2
    		3
    ，AC=4，D为PC的中点，PB⊥AD．
    （1）证明：BC⊥AB；
    （2）求二面角B-AD-C大小的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在圆内画1条线段，将圆分割成两部分；画2条相交线段，将圆分割成4部分；画3条线段，将圆最多分割成7部分；画4条线段，将圆最多分割成11部分．

    （1）记在圆内画n条线段，将圆最多分割成an部分，归纳出an+1与an的关系；
    （2）猜想数列{an}的通项公式，根据an+1与an的关系及数列的知识，证明你的猜想是否成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f（x）=sinx|sinx-a|-4，若a=1时，f（x）的最小值是
     
    ；若对任意x∈[0，
    π
    2
    ]，f（x）≤0恒成立，则实数a的取值范围是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    有5个不同的小球，其中红色球有2个，黄色球有2个，蓝色球有1个，若将其随机的排成一列，但要求同一颜色的小球不相邻，则不同的排列种数为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    观察下列等式：照此规律，第n个等式可为
     
    ．
    2=1×2
    2+4=2×3
    2+4+6=3×4
    2+4+6+8=4×5
    …

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设非零向量
    a
    ，
    b
    满足|
    a
    |=1，|
    a
    +2
    b
    |=1，则|
    a
    +
    b
    |+|
    b
    |的取值范围为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    圆ρ=sinθ-cosθ（ρ＞0，0≤θ＜2π）的圆心的极坐标是
     
    ．

    查看答案和解析>>

    同步练习册答案