
(2014·郑州模拟)已知函数f(x)=ex+ax,g(x)=ax-lnx,其中a≤0.
(1)求f(x)的极值.
(2)若存在区间M,使f(x)和g(x)在区间M上具有相同的单调性,求a的取值范围.
(1)f(x)的极小值为f(ln(-a))=-a+aln(-a);没有极大值
(2)(-∞,-1)
【解析】(1)f(x)的定义域为R,且f′(x)=ex+a.
当a=0时,f(x)=ex,故f(x)在R上单调递增.
从而f(x)没有极大值,也没有极小值.
当a<0时,令f′(x)=0,得x=ln(-a).
f(x)和f′(x)的情况如下:
x | (-∞,ln(-a)) | ln(-a) | (ln(-a),+∞) |
f′(x) | - | 0 | + |
f(x) | ↘ |
| ↗ |
故f(x)的单调递减区间为(-∞,ln(-a));
单调递增区间为(ln(-a),+∞).
从而f(x)的极小值为f(ln(-a))=-a+aln(-a);没有极大值.
(2)g(x)的定义域为(0,+∞),且g′(x)=a- =
= .
.
当a=0时,f(x)在R上单调递增,
g(x)在(0,+∞)上单调递减,不合题意.
当a<0时,g′(x)<0,g(x)在(0,+∞)上单调递减.
当-1≤a<0时,ln(-a)≤0,
此时f(x)在(ln(-a),+∞)上单调递增,
由于g(x)在(0,+∞)上单调递减,不合题意.
当a<-1时,ln(-a)>0,
此时f(x)在(-∞,ln(-a))上单调递减,
由于g(x)在(0,+∞)上单调递减,符合题意.
综上,a的取值范围是(-∞,-1).


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源:2014年高考数学人教版评估检测 第十章 算法初步、统计、统计案例(解析版) 题型:选择题
口袋内装有一些大小相同的红球、白球和黑球,从中摸出1个球,摸出红球的概率是0.42,摸出白球的概率是0.28,那么摸出黑球的概率是( )
A.0.42 B.0.28 C.0.3 D.0.7
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第八章 平面解析几何(解析版) 题型:选择题
(2013·四川高考)从椭圆 +
+ =1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
=1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第五章 数列(解析版) 题型:填空题
在等比数列{an}中,a1=1,公比为q,且|q|≠1.若am=a1a2a3a4a5,则m=__________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第五章 数列(解析版) 题型:选择题
(2014·郑州模拟)等差数列{an}中,2a3-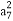 +2a11=0,数列{bn}是等比数列,且b7=a7,则b6b8=( )
+2a11=0,数列{bn}是等比数列,且b7=a7,则b6b8=( )
A.2 B.4 C.8 D.16
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第二章 函数、导数及其应用(解析版) 题型:填空题
(2014·哈尔滨模拟)已知函数f(x)=x2+ ,g(x)=
,g(x)= -m.若?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是__________.
-m.若?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是__________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第二章 函数、导数及其应用(解析版) 题型:选择题
(2014·沈阳模拟)已知符号函数sgn(x)=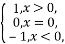 则函数f(x)=sgn(lnx)-lnx的零点个数为( )
则函数f(x)=sgn(lnx)-lnx的零点个数为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布(解析版) 题型:选择题
一个样本容量为10的样本数据,它们组成一个公差不为0的等差数列{an},若a3=8且a1,a3,a7成等比数列,则此样本的平均数和中位数分别是( )
A.13,12 B.13,13 C.12,13 D.13,14
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第七章 立体几何(解析版) 题型:选择题
圆台上、下底面面积分别是π,4π,侧面积是6π,这个圆台的体积是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com