
| A. | {m|m>$\frac{9}{4}$} | B. | {m|m≥$\frac{9}{4}$} | C. | {m|m<$\frac{9}{4}$} | D. | {m|m≤$\frac{9}{4}$} |
分析 利用“乘1法”与基本不等式的性质求解$\frac{1}{x}$+$\frac{4}{y}$的最小值可得答案.
解答 解:x>0,y>0且x+y=4,
则:$\frac{x}{4}+\frac{y}{4}=1$,
那么($\frac{1}{x}$+$\frac{4}{y}$)($\frac{x}{4}+\frac{y}{4}$)=$\frac{1}{4}$+1$+\frac{x}{y}+\frac{y}{4x}$≥$\frac{5}{4}$$+2\sqrt{\frac{x}{y}•\frac{y}{4x}}$=$\frac{9}{4}$,当且仅当2x=y=$\frac{8}{3}$时取等号.
∴$\frac{1}{x}$+$\frac{4}{y}$的最小值为$\frac{9}{4}$.
要使不等式$\frac{1}{x}$+$\frac{4}{y}$≥m恒成立,
∴m$≤\frac{9}{4}$.
故选D.
点评 本题考查了“乘1法”与基本不等式的性质的运用,属于中档题.


科目:高中数学 来源: 题型:解答题
 函数f(x)是R上的奇函数,且当x>0时,函数的解析式为f(x)=log2(x+1).
函数f(x)是R上的奇函数,且当x>0时,函数的解析式为f(x)=log2(x+1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
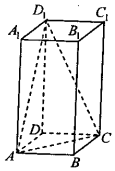 在正四棱柱ABCD-A1B1C1D1中,AB=2,BB1=4,则BB1与平面ACD1所成角的正弦值为( )
在正四棱柱ABCD-A1B1C1D1中,AB=2,BB1=4,则BB1与平面ACD1所成角的正弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,5) | B. | (1,1) | C. | (3,1) | D. | (3,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | 1 | C. | $\frac{3}{5}$ | D. | $\frac{50}{27}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com