
(本小题满分12分)
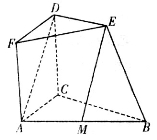
如图,四边形ACDF为正方形,平面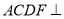 平面BCDE,平面
平面BCDE,平面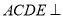 平面ABC,BC=2DE,DE//BC, M为AB的中点.
平面ABC,BC=2DE,DE//BC, M为AB的中点.
(I)证明: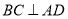 ;
;
(II)证明:EM//平面ACDF.
(Ⅰ)详见解析; (Ⅱ)详见解析
【解析】
试题分析:(Ⅰ)首先根据面面垂直的性质定理,可得AC⊥平面BCDE,进而得到AC⊥BC,同理可得DC⊥平面ABC,即可得到DC⊥BC,再利用面面垂直的判定定理,即可证明结论.
(Ⅱ)(法一)取BC的中点为N,连结MN,EN,由中位线定理,可得MN∥AC,又DE∥BC,且DE =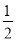 BC= CN,可得四边形CDEN为平行四边形,即可得到EN∥DC,平面EMN∥平面ACD, 利用面面平行的性质定理即可证明结论.(法二)取AC的中点P,连结PM,PD 在△ABC中,P为AC的中点,M为AB的中点,∴PM∥BC,且PM=
BC= CN,可得四边形CDEN为平行四边形,即可得到EN∥DC,平面EMN∥平面ACD, 利用面面平行的性质定理即可证明结论.(法二)取AC的中点P,连结PM,PD 在△ABC中,P为AC的中点,M为AB的中点,∴PM∥BC,且PM= BC,又∵DE∥BC,DE=
BC,又∵DE∥BC,DE= BC,∴
BC,∴ ,根据线面平行的判定定理即可证明结论.
,根据线面平行的判定定理即可证明结论.
试题解析:证明:(Ⅰ)∵平面ACDF⊥平面BCDE,平面ACDF∩平面BCDE= DC,
又正方形ACDF中,AC⊥DC,∴AC⊥平面BCDE,
∴AC⊥BC.
又∵平面ACDF⊥平面ABC,平面ACDF∩平面ABC =AC,DC⊥AC,
∴DC⊥平面ABC,∴DC⊥BC.
又∵AC∩DC =C,∴BC⊥平面ACDF,
而AD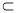 面ACDF,
面ACDF,
∴BC⊥AD.
(Ⅱ)(法一)如图,取BC的中点为N,连结MN,EN.
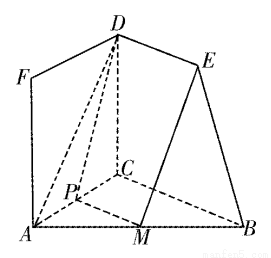
在△ABC中,M为AB的中点,N为BC的中点,
∴MN∥AC,
又DE∥BC,且DE = 1BC= CN,
∴四边形CDEN为平行四边形,
∴EN∥DC,
∴平面EMN∥平面ACD,
又∵EM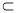 平面EMN,
平面EMN,
∴EM//面ACDF.
(法二)如图,取AC的中点P,连结PM,PD
在△ABC中,P为AC的中点,M为AB的中点,
∴PM∥BC,且PM= BC,
BC,
又∵DE∥BC,DE= BC,
BC,
∴ .
.
故四边形DEMP为平行四边形,∴ME∥DP,
又∵DP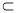 面ACDF,∴EM∥平面ACDF.
面ACDF,∴EM∥平面ACDF.
考点:1.面面垂直的判定定理和性质定理;2.线面平行的判定定理;3.面面平行的性质定理.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源:2014-2015学年吉林省长春市高三质量监测(二)理科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-5:不等式选讲
设函数 ,
, .
.
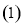 当
当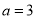 时,求不等式
时,求不等式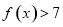 的解集;
的解集;
 对任意
对任意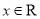 恒有
恒有 ,求实数
,求实数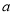 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省资阳市高三第二次诊断性考理科数学试卷(解析版) 题型:选择题
设抛物线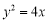 上的一点P到y轴的距离是4,则点P到该抛物线焦点的距离为( )
上的一点P到y轴的距离是4,则点P到该抛物线焦点的距离为( )
(A)3 (B)4
(C)5 (D)6
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市青浦区高三上学期期终学习质量调研数学试卷(解析版) 题型:填空题
若甲乙两人从 门课程中各选修
门课程中各选修 门,则甲乙所选的课程中恰有
门,则甲乙所选的课程中恰有 门相同的选法有 种.
门相同的选法有 种.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省潍坊市高三上学期期末考试文科数学试卷B卷(解析版) 题型:填空题
在 中,角A,B。C的对边分别为
中,角A,B。C的对边分别为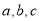 .已知
.已知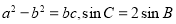 ,则角A为__________.
,则角A为__________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省潍坊市高三上学期期末考试文科数学试卷B卷(解析版) 题型:选择题
已知某几何体的三视图如图所示,则该几何体的外接球的表面积为( )
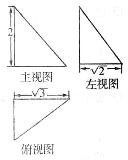
A. 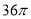 B.
B. 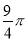 C.
C. 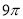 D.
D. 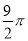
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省青岛市高三上学期期末考试理科数学试卷(解析版) 题型:选择题
若圆台两底面周长的比是1:4,过高的中点作平行于底面的平面,则圆台被分成两部分的体积比是
A.1:16 B.39:129 C.13:129 D.3:27
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com