练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．若样本数据x1，x2，…，x10的平均数为8，则数据2x1-1，2x2-1，…，2x10-1的平均数为15．

    分析 根据平均数与方差的公式即可求出数据2x1-1，2x2-1，…，2x10-1的平均数．

    解答 解：∵样本数据x1，x2，…，x10的平均数是10，
    ∴$\overline{x}$=$\frac{1}{10}$（x1+x2+…+x10）=8；
    ∴数据2x1-1，2x2-1，…，2x10-1的平均数是：
    $\overline{x′}$=$\frac{1}{10}$[（2x1-1）+（2x2-1）+…+（2x10-1）]
    =2×$\frac{1}{10}$（x1+x2+…+x10）-1=2×8-1=15．
    故答案为：15．

    点评 本题考查了计算数据的平均数问题，解题时应根据公式进行计算，也可以利用平均数的性质直接得出答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右顶点为A，x轴上有一点Q（2a，0），若C上存在一点P，使AP⊥PQ，则双曲线离心率的取值范围是（　　）
    A．$e＞\frac{{\sqrt{6}}}{2}$B．$1＜e＜\frac{{\sqrt{6}}}{2}$C．$e≥\frac{{\sqrt{6}}}{3}$D．$1＜e＜\frac{{\sqrt{6}}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数f（x）=|x-a|，其中a＞1．
    （1）当a=3时，求不等式f（x）≥4-|x-4|的解集；
    （2）若函数h（x）=f（2x+a）-2f（x）的图象与x、y轴围成的三角形面积大于a+4，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

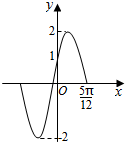    19．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则下列判断错误的是（　　）
    A．f（$\frac{π}{3}$）=1
    B．函数f（x）的图象关于x=$\frac{7π}{6}$对称
    C．函数f（x）的图象关于（-$\frac{11π}{2}$，0）对称
    D．函数f（x）的图象向右平移$\frac{π}{12}$个单位后得到y=Asinωx的图象

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

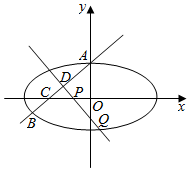    6．已知椭圆$G：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的长轴长为4，离心率$e=\frac{{\sqrt{3}}}{2}$．
    （Ⅰ）求椭圆G的方程；
    （Ⅱ）设过椭圆G的上顶点A的直线l与椭圆G的另一个交点为B，与x轴交于点C，线段AB的中点为D，线段AB的垂直平分线分别交x轴、y轴于P、Q两点．问：是否存在直线l使△PDC与△POQ的面积相等（O为坐标原点）？若存在，求出所有满足条件的直线l的方程；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．设函数$f（x）=\left\{\begin{array}{l}\frac{1}{x}，x＞1\\-x-2，x≤1\end{array}\right.$，则f[f（2）]=-$\frac{5}{2}$，不等式$f（a）＞\frac{1}{2}$的解集是（-∞，-$\frac{5}{2}$）∪（1，2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知集合A={x|x2≥16}，B={m}，若A∪B=A，则实数m的取值范围是（　　）
    A．（-∞，-4）B．[4，+∞）C．[-4，4]D．（-∞，-4]∪[4，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．设变量x，y满足约束条件$\left\{\begin{array}{l}{x+y-2≥0}\\{x-y≥0}\\{2x-y-4≤0}\end{array}\right.$，则目标函数z=2x+y的最大值为（　　）
    A．3B．4C．6D．12

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知等差数列{an}公差为d，前n项和{sn}，则下列描述不一定正确的是（　　）
    A．若a1＞0，d＞0，则n唯一确定时$s_n^{\;}$也唯一确定
    B．若a1＞0，d＜0，则n唯一确定时$s_n^{\;}$也唯一确定
    C．若a1＞0，d＞0，则$s_n^{\;}$唯一确定时n也唯一确定
    D．若a1＞0，d＜0，则$s_n^{\;}$唯一确定时n也唯一确定

    查看答案和解析>>

    同步练习册答案