
【题目】(2015![]() 福建)已知函数
福建)已知函数![]() =
=![]() .
.
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)证明:当x>1时,![]()
![]() ;
;
(3)确定实数k的所有可能取值,使得存在![]() ,当
,当![]() 时,恒有
时,恒有![]() >
>![]() .
.
【答案】
(1)
![]() ;
;
(2)
详见解析;
(3)
![]() .
.
【解析】(1)![]() ,x
,x![]()
![]() . 由
. 由![]() >0得
>0得![]() ,解得0<x<
,解得0<x<![]() .故
.故![]() 的单调递增区间是
的单调递增区间是![]() 。
。
(2)令![]() =
=![]()
![]() ,x
,x![]()
![]() ,则有
,则有![]() =
=![]() .当x
.当x![]()
![]() 时,
时,![]() <0, 所以
<0, 所以![]() 在[1,+
在[1,+![]() )上单调递减,故x>1时,
)上单调递减,故x>1时,![]() <
<![]() =0,即当x>1时,
=0,即当x>1时,![]()
![]() ;
;
(3)由(2)知,当k=1时,不存在![]() 满足题意。 当k>1时,有
满足题意。 当k>1时,有![]()
![]() <
<![]() ,则
,则![]() <
<![]() ,从而不存在
,从而不存在![]() 满足题意 。 当k<1时,令G(x)=
满足题意 。 当k<1时,令G(x)=![]() -
-![]() ,x
,x![]()
![]() . 则有
. 则有![]() =
=![]()
![]() =
=![]() . 由
. 由![]() =0得,
=0得, ![]() , 解得
, 解得![]() <0,
<0,![]() >1. 当x
>1. 当x![]()
![]() 时,
时,![]() =0,即
=0,即![]() >
>![]() ,综上k的取值范围是
,综上k的取值范围是![]() .
.
【考点精析】关于本题考查的函数单调性的判断方法,需要了解单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】(2015·四川)如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ上,E、F分别为AB、BC的中点。设异面直线EM与AF所成的角为![]() ,则cos
,则cos![]() 的最大值为 .
的最大值为 .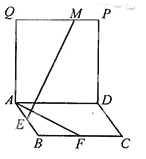
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
(Ⅰ)求证:BE//平面ADE ;
(Ⅱ)求平面AEF与平面BEC所成锐二面角的余弦值.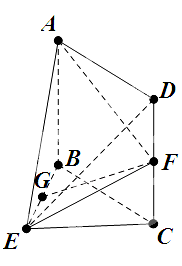
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖北)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
如图,在阳马P-ABCD中,侧棱![]() 底面
底面![]() ,且
,且![]() ,过棱
,过棱![]() 的中点
的中点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]()
(1)证明:![]() 平面
平面![]() .试判断四面体
.试判断四面体![]() 是否为鳖臑,若是,写出其每个面的直角(只需写
是否为鳖臑,若是,写出其每个面的直角(只需写
出结论);若不是,说明理由;
(2)若面![]() 与面
与面![]() 所成二面角的大小为
所成二面角的大小为![]() , 求
, 求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标.根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.求:(1)现从融合指数在[4,5)和[7,8]内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在[7,8]的概率;(2)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.
全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标.根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.求:(1)现从融合指数在[4,5)和[7,8]内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在[7,8]的概率;(2)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.
组号 | 分组 | 频数 |
1 | [4,5) | 2 |
2 | [5,6) | 8 |
3 | [6,7) | 7 |
4 | [7,8] | 3 |
(1)现从融合指数在[4,5)和[7,8]内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在[7,8]的概率;
(2)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()
(Ⅰ)求频率分布图中a的值;
(Ⅱ)估计该企业的职工对该部门评分不低于80的概率;
(Ⅲ)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率。
的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥V-ABC中,平面VAB![]() 平面ABC,
平面ABC,![]() VAB为等比三角形,AC
VAB为等比三角形,AC![]() BC且AC=BC=
BC且AC=BC=![]() ,O,M分别为AB,VA的中点。
,O,M分别为AB,VA的中点。
(I)求证:VB//平面MOC;
(II)求证:平面MOC![]() 平面VAB;
平面VAB;
(III)求三棱锥V-ABC的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( ) 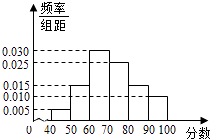
A.588
B.480
C.450
D.120
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com