
已知等差数列{an}的前n项和为Sn,且满足Sn=n2﹣n.
(1)求an;
(2)设数列{bn}满足bn+1=2bn﹣an且b1=4,
(i)证明:数列{bn﹣2n}是等比数列,并求{bn}的通项;
(ii)当n≥2时,比较bn﹣1•bn+1与bn2的大小.
(1)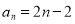 ;(2)(i)
;(2)(i)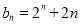 ,(ii)当
,(ii)当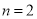 或
或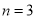 时,
时,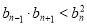 ,当
,当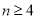 时,
时,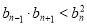 .
.
【解析】
试题分析:
解题思路:(1)利用 求解即可;(2)(i)由
求解即可;(2)(i)由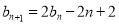 构造新数列
构造新数列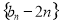 ,并证明新数列为等比数列,进一步求
,并证明新数列为等比数列,进一步求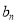 ;(ii)利用作差法判定两式的大小.
;(ii)利用作差法判定两式的大小.
规律总结:求数列的通项公式一般有三种类型:①利用等差数列、等比数列的基本量求通项公式;②已知数列的首项与递推式,求通项公式;③利用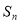 与
与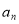 的关系求通项公式;比较大小,往往使用作差法.
的关系求通项公式;比较大小,往往使用作差法.
试题解析:(1)当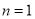 时
时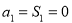 ;当
;当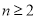 时,
时,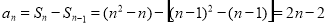 ;
;
 满足上式,
满足上式,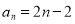
(2)(i)由已知得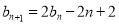 ,即
,即 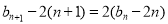 .且
.且 ,
,
所以数列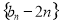 是以2为首项,2为公比的等比数列 ,
是以2为首项,2为公比的等比数列 ,
则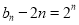 ,所以
,所以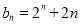 ;
;
(ii)当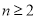 时,
时,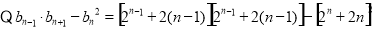
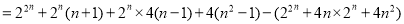
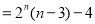 ,
,
所以当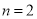 或
或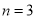 时,
时,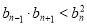 ,当
,当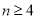 时,
时,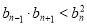 .
.
考点:1.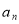 与
与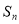 的关系;2.等比数列;3.不等式的证明.
的关系;2.等比数列;3.不等式的证明.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源:2016届湖北武汉蔡甸区第二中学高一下六科竞赛数学文试卷(解析版) 题型:选择题
用火柴棒摆“金鱼”,按照上面的规律,第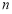 个“金鱼”图需要火柴棒的根数为( )
个“金鱼”图需要火柴棒的根数为( )
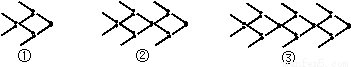
A.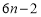 B.
B.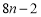 C.
C.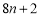 D.
D. 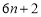 .
.
查看答案和解析>>
科目:高中数学 来源:2016届浙江省金华市高一下学期期末考试数学试卷(解析版) 题型:选择题
已知x,y均为正数且x+2y=xy,则( ).
A.xy+ 有最小值4 B.xy+
有最小值4 B.xy+ 有最小值3
有最小值3
C.x+2y+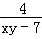 有最小值11 D.xy﹣7+
有最小值11 D.xy﹣7+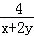 有最小值11
有最小值11
查看答案和解析>>
科目:高中数学 来源:2016届浙江省诸暨市高一下学期期中考试数学试卷(解析版) 题型:填空题
设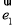 ,
,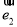 为单位向量, 且
为单位向量, 且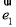 ,
, 的夹角为
的夹角为 ,若
,若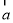 =
=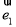 +3
+3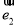 ,
,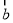 =2
=2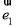 ,则向量
,则向量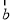 在
在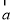 方向上的投影为________.
方向上的投影为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com