
分析 (Ⅰ)若$\frac{f(0)}{|a|}$≥1,则$\frac{-a\left|a\right|}{|a|}$≥1,解得a的取值范围;
(Ⅱ)结合二次函数的图象和性质,分类讨论,可得f(x)的最小值;
(Ⅲ)设函数h(x)=f(x),x∈(a,+∞),即3x2-2ax+a2-1≥0,分类可得不同情况下不等式h(x)≥1的解集.
解答 解:(Ⅰ)∵$\frac{f(0)}{|a|}$≥1,
∴$\frac{-a\left|a\right|}{|a|}$≥1,
即-a≥1,
∴a≤-1;…3分
(Ⅱ)(1)当x≥a时,f(x)=3x2-2ax+a2,函数的图象是开口朝上,且以直线x=$\frac{a}{3}$为对称轴,
此时,f(x)min=$\left\{\begin{array}{l}f(a),a≥0\\ f(\frac{a}{3}),a<0\end{array}\right.$=$\left\{\begin{array}{l}2{a}^{2},a≥0\\ \frac{2{a}^{2}}{3},a<0\end{array}\right.$,…5分
(2)当x<a时,f(x)=x2+2ax-a2,函数的图象是开口朝上,且以直线x=-a为对称轴,
此时,f(x)min=$\left\{\begin{array}{l}f(-a),a≥0\\ f(a),a<0\end{array}\right.$=$\left\{\begin{array}{l}-2{a}^{2},a≥0\\ 2{a}^{2},a<0\end{array}\right.$,…6分
综上,f(x)min=$\left\{\begin{array}{l}-2{a}^{2},a≥0\\ \frac{2{a}^{2}}{3},a<0\end{array}\right.$;…7分
(Ⅲ)当x∈(a,+∞)时,
由h(x)≥1得:3x2-2ax+a2-1≥0,
∵△=4a2-12(a2-1)=12-8a2,
(1)当△≤0,即a≤-$\frac{\sqrt{6}}{2}$或a≥$\frac{\sqrt{6}}{2}$时,x∈(a,+∞);
(2)当△>0,即-$\frac{\sqrt{6}}{2}$<a<$\frac{\sqrt{6}}{2}$时,得$\left\{\begin{array}{l}(x-\frac{a-\sqrt{3-2{a}^{2}}}{3})(x-\frac{a+\sqrt{3-2{a}^{2}}}{3})≥0\\ x>a\end{array}\right.$,
综上:当a∈(-$\frac{\sqrt{6}}{2}$,-$\frac{\sqrt{2}}{2}$)时,解集为:$(a,\frac{a-\sqrt{3-2{a}^{2}}}{3}]∪[\frac{a+\sqrt{3-2{a}^{2}}}{3},+∞)$,
当a∈[-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$]时,解集为:$[\frac{a+\sqrt{3-2{a}^{2}}}{3},+∞)$,
当a∈($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{6}}{2}$)时,解集为:(a,+∞).…12分.
点评 本题考查的知识点是分段函数的应用,函数的最值及其几何意义,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
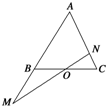 如图所示,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点M,N,若$\overrightarrow{AB}$=m$\overrightarrow{AM}$,$\overrightarrow{AC}$=n$\overrightarrow{AN}$ (m,n>0),则m2+n的范围为[$\frac{7}{4}$,4).
如图所示,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点M,N,若$\overrightarrow{AB}$=m$\overrightarrow{AM}$,$\overrightarrow{AC}$=n$\overrightarrow{AN}$ (m,n>0),则m2+n的范围为[$\frac{7}{4}$,4).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com