
分析 (1)将原不等式等价转化后,由一元二次不等式和解法求出解集,并用穿根法借助于数轴画出来;
(2)将原不等式去掉绝对值,转化为一元二次不等式组,由一元二次不等式的解法求出解集;
(3)通分后将原不等式等价转化,利用穿根法借助于数轴画出图象,再求出解集.
解答 解:(1)原不等式等价于(x+4)(x+5)2(x-2)3>0,
∴$\left\{\begin{array}{l}{x≠5}\\{(x+4)(x-2)>0}\end{array}\right.$,解得x<-4或x>2且x≠-5,
如图所示:
∴原不等式解集为{x|x<-4或x>2且x≠-5};
(2)将|4x2-10x-3|<3去掉绝对值号得,
-3<4x2-10x-3<3,
∴原不等式等价于不等式组$\left\{\begin{array}{l}{4{x}^{2}-10x>0}\\{4{x}^{2}-10x-6<0}\end{array}\right.$,
则$\left\{\begin{array}{l}{2x(2x-5)>0}\\{2(x-3)(2x+1)<0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x<0或x>\frac{5}{2}}\\{-\frac{1}{2}<x<3}\end{array}\right.$,
∴原不等式的解集为{x|$-\frac{1}{2}<x<0$或$\frac{5}{2}<x<3$};
(3)由$\frac{{x}^{2}-4x+1}{3{x}^{2}-7x+2}<1$ 得,$\frac{{-2x}^{2}+3x-1}{3{x}^{2}-7x+2}<0$,
∴原不等式等价于$\frac{(2x-1)(x-1)}{(3x-1)(x-2)}>0$,即(2x-1)(x-1)(3x-1)(x-2)>0,
如图所示:
∴原不等式解集为{x|x $<\frac{1}{3}$或$\frac{1}{2}<x<1$ 或x>2}.
点评 本题考查高次不等式、绝对值不等式、分式不等式的等价转化问题,一元二次不等式的解法,以及穿根法的应用,考查数形结合思想,转化思想,化简、变形能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
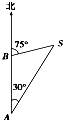 (文)如图,一艘船上午9:30在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,上午10:00到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距8$\sqrt{2}$ n mile.求此船的航速.
(文)如图,一艘船上午9:30在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,上午10:00到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距8$\sqrt{2}$ n mile.求此船的航速.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上一年的出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 下一年的保费倍率 | 0.85 | 1 | 1.25 | 1.5 | 1.75 | 2 |
| 连续两年没有出险打7折,连续三年没有出险打6折 | ||||||
| 一年中的出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 频数 | 500 | 380 | 100 | 15 | 4 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 | 6 | … |
| f(x) | 5 | 1 | 3 | 2 | 6 | 4 | … |
| A. | 1 | B. | 2 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3) | B. | (-∞,-3] | C. | (-3,+∞) | D. | [-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=lgx2,g(x)=2lgx | B. | y=f(x),y=f(x+1) | ||
| C. | $f(u)=\sqrt{\frac{1+u}{1-u}},f(v)=\sqrt{\frac{1+v}{1-v}}$ | D. | $f(x)=x,g(x)=\sqrt{x^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,D为PC的中点,E为PB的中点.
如图,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,D为PC的中点,E为PB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com