
分析 (1)直接利用函数的单调性的定义证明判断即可.
(2)利用(1)的结果,求出函数的最值,列出方程求解即可.
解答 解:(1)函数f(x)在[0,+∞)上是单调增函数.
证明如下:任取x1,x2∈[0,+∞),且x1<x2,则$f({x_1})-f({x_2})=2-\frac{3}{{{x_1}+1}}-(2-\frac{3}{{{x_2}+1}})=\frac{{3({x_1}-{x_2})}}{{({x_1}+1)({x_2}+1)}}$
因为x1,x2∈[0,+∞),且x1<x2,所以f(x1)-f(x2)<0,即f(x1)<f(x2).
所以f(x)在[0,+∞)上是单调增函数.
(2)由(1)知f(x)在[1,m]递增,所以$f(m)-f(1)=\frac{1}{2}$,即:$\frac{2m-1}{m+1}$-$\frac{1}{2}$=$\frac{1}{2}$,所以m=2.
点评 本题考查函数的单调性的判断与应用,函数的最值的求法,考查计算能力.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:填空题
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+6 | 5 | 6 | 7 | 8 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
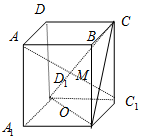 如图ABCD-A1B1C1D1是长方体,O是B1D1的中点,直线AC1交平面CB1D1于点M,则下列结论正确的是( )
如图ABCD-A1B1C1D1是长方体,O是B1D1的中点,直线AC1交平面CB1D1于点M,则下列结论正确的是( )| A. | C,M,O三点共线 | B. | C,M,O,A1不共面 | C. | A,M,O,C不共面 | D. | B,M,O,B1共面 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com