
已知函数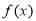 =
=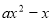 (
(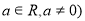 ,
,
(1)当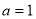 时,判断函数
时,判断函数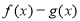 在定义域上的单调性;
在定义域上的单调性;
(2)若函数 与
与 的图像有两个不同的交点
的图像有两个不同的交点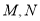 ,求
,求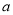 的取值范围。
的取值范围。
(3)设点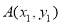 和
和 (
(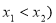 是函数
是函数 图像上的两点,平行于
图像上的两点,平行于 的切线以
的切线以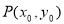 为切点,求证
为切点,求证 .
.
(1)在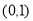 上单调递减,在
上单调递减,在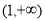 上单调递增;(2)
上单调递增;(2)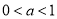 ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题分析:
解题思路:(1)求导,利用导数的正负确定函数的单调区间;(2)构造函数,将图像的交点个数转化为函数的零点个数,通过函数的极值的正负求参数的值;(3)构造函数,利用放缩法合理转化.
规律总结:利用导数研究函数的单调性、极值、最值及与函数有关的综合题,都体现了导数的重要性;此类问题往往从求导入手,思路清晰;但综合性较强,需学生有较高的逻辑思维和运算能力.
试题解析:(1)记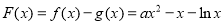 ,则
,则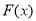 的定义域为
的定义域为 .
.
当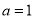 时,
时,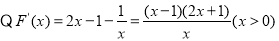 ,
,
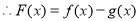 在
在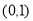 上单调递减,在
上单调递减,在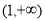 上单调递增.
上单调递增.
由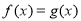 得
得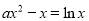 ,即
,即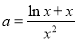 ,
,
令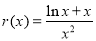 ,
,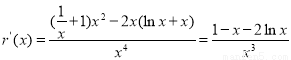 ;
;
当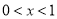 时,
时,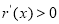 ,则
,则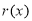 单调递增,且
单调递增,且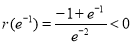 ;
;
当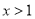 时,
时, ,则
,则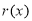 单调递减,且
单调递减,且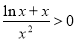 ,
,
所以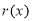 在
在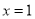 处取到最大值
处取到最大值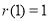 ;
;
故要使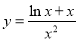 与
与 有两个不同的交点,只需
有两个不同的交点,只需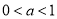 .
.
(3)由已知: ,所以
,所以
由
 ,故
,故
同理
综上所述得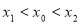 .
.
考点:1.函数的单调性;2.函数的零点;3.放缩法.


科目:高中数学 来源:2015数学一轮复习迎战高考:10-6几何概型(解析版) 题型:填空题
某公共汽车站每隔10分钟有一辆汽车到达,乘客到达车站的时刻是任意的,则一个乘客候车时间不超过7分钟的概率是________.

查看答案和解析>>
科目:高中数学 来源:2015数学一轮复习迎战高考1-3简单逻辑联结词、全称量词与存在量词(解析版) 题型:选择题
[2014·河南洛阳模拟]下列命题中的假命题是( )
A.?x∈R,2x-1>0 B.?x∈N*,(x-1)2>0
C.?x∈R,lgx<1 D.?x∈R,tanx=2
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
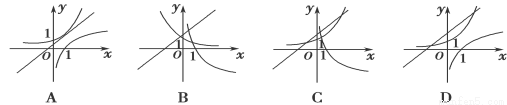
在同一坐标系中画出函数y=logax,y=ax,y=x+a的图象,可能正确的是( ).
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知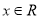 ,则“
,则“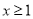 ”是“
”是“ ”的( ).
”的( ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试文科数学试卷(解析版) 题型:填空题
若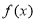 是定义在R上的奇函数,且满足
是定义在R上的奇函数,且满足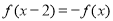 ,给出下列4个结论:
,给出下列4个结论:
(1)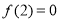 ; (2)
; (2)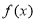 是以4为周期的函数;
是以4为周期的函数;
(3)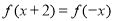 ; (4)
; (4)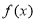 的图像关于直线
的图像关于直线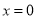 对称;
对称;
其中所有正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
函数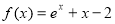 的零点所在的一个区间是( ).
的零点所在的一个区间是( ).
A、(-2,-1) B、(-1,0) C、(0,1) D、(1,2)
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末理科数学试卷(解析版) 题型:解答题
已知全集U=R,集合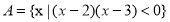 ,函数
,函数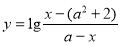 的定义域为集合B.
的定义域为集合B.
(1)若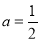 时,求集合
时,求集合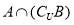 ;
;
(2)命题P: 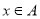 ,命题q:
,命题q: 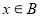 ,若q是p的必要条件,求实数a的取值范围.
,若q是p的必要条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com