Question

2．某种产品的广告费支出x与销售额y（单位：百万元）之间有如下对应数据：

x	2	4	5	6	8
y	30	40	60	50	70

（1）画出散点图；
（2）求回归直线方程；
（3）试预测广告支出为10百万元时，销售额多大？
（注：b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{x}^{2}}$，a=$\overline{y}-b\overline{x}$．

Answer 1

分析 （1）根据表中所给的五组数据，得到五个点的坐标，在平面直角坐标系中画出散点图．
（2）先求出横标和纵标的平均数，得到这组数据的样本中心点，利用最小二乘法求出线性回归方程的系数，代入样本中心点求出a的值，写出线性回归方程．
（3）将x=10代入回归直线方程求出y的值即为当广告费支出10（百万元）时的销售额的估计值．

解答 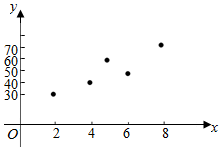解：（1）根据表中所列数据可得散点图如图：
（2）$\overline{x}$=5，$\overline{y}$=50，$\sum_{i=1}^{5}$${{x}_{i}}^{2}$=145，$\sum_{i=1}^{5}$${{y}_{i}}^{2}$=13500，$\sum_{i=1}^{5}$x_iy_i=1380，
∴b=$\frac{1380-5×5×50}{145-5×{5}^{2}}$=6.5，a=50-6.5×5=17.5，
∴y=6.5x+17.5；
（3）x=10时，y=6.5×10+17.5=82.5（百万元）．

点评 本题考查线性回归方程的求法和应用，本题解题的关键是利用最小二乘法求出线性回归方程的系数，这是解答正确的主要环节．