
| 休闲方式 性别 |
看电视 | 运动 | 合计 |
| 女 | 43 | 27 | 70 |
| 男 | 21 | 33 | 54 |
| 合计 | 64 | 60 | 124 |
| 124(43×33-27×21)2 |
| 70×54×64×60 |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 |
| k0 | 3.841 | 5.024 | 6.635 |
| A、①③ | B、①④ | C、②③ | D、②④ |
科目:高中数学 来源: 题型:
| (k-3)π |
| 3 |
| (-21-k)π |
| 3 |
| A、P?Q | B、P?Q |
| C、P=Q | D、P∩Q=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知定义在R上的函数f(x),其导函数y=f′(x)的大致图象如图所示,则下列叙述正确的是( )
已知定义在R上的函数f(x),其导函数y=f′(x)的大致图象如图所示,则下列叙述正确的是( )| A、f(a)取得极小值 |
| B、f(d)取得最小值 |
| C、f(x)在(a,c)上单调递增 |
| D、f(e)取得极大值 |
查看答案和解析>>
科目:高中数学 来源: 题型:
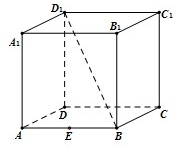 正方体AC1中,E为AB的中点,点P为侧面BB1C1C内一动点(含边界),若动点P始终满足PE⊥BD1,则动点P的轨迹是( )
正方体AC1中,E为AB的中点,点P为侧面BB1C1C内一动点(含边界),若动点P始终满足PE⊥BD1,则动点P的轨迹是( )| A、直线 | B、线段 |
| C、圆的一部分 | D、椭圆的一部分 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、1+
| ||
C、
| ||
D、1+
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com