Question

6．将正方形ABCD沿对角线BD折成直二面角A-BD-C，有如下四个结论：
?①AC⊥BD；?
②△ACD是等边三角形；
?③AB与平面BCD成60°的角；
④AB与CD所成的角是90°．
其中正确结论的序号是①②．

Answer 1

分析 由题意画出图形，然后利用线面垂直的判定和性质判断①；求出AC长度判断②；由图求得AB与平面BCD所成角判断③；利用反证法说明④错误．

解答 解：如图，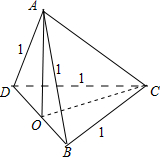

设正方形ABCD的边长为1，BD中点为O，连接AO，CO，
则AO⊥BD，CO⊥BD，∴BD⊥平面AOC，则AC⊥BD，故①正确；
由平面ABD⊥平面BCD，且AO⊥BD，得AO⊥平面BCD，
∴AO⊥CO，则AC=$\sqrt{（\frac{\sqrt{2}}{2}）^{2}+（\frac{\sqrt{2}}{2}）^{2}}=1$，则△ACD是等边三角形，故②正确；
AB与平面BCD所成角为∠ABO=45°，故③错误；
若AB与CD所成的角是90°，即AB⊥CD，又AO⊥CD，∴CD⊥平面ADB，而CO⊥平面ADB，故④错误．
∴正确结论的序号是①②．
故答案为：①②．

点评 本题考查空间中位置关系的判定，考查空间想象能力和思维能力，是中档题．