
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:解答题
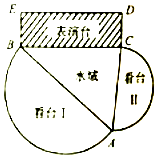 在水域上建一个演艺广场,演艺广场由看台Ⅰ,看台Ⅱ,三角形水域ABC,及矩形表演台BCDE四个部分构成(如图),看台Ⅰ,看台Ⅱ是分别以AB,AC为直径的两个半圆形区域,且看台Ⅰ的面积是看台Ⅱ的面积的3倍,矩形表演台BCDE 中,CD=10米,三角形水域ABC的面积为$400\sqrt{3}$平方米,设∠BAC=θ.
在水域上建一个演艺广场,演艺广场由看台Ⅰ,看台Ⅱ,三角形水域ABC,及矩形表演台BCDE四个部分构成(如图),看台Ⅰ,看台Ⅱ是分别以AB,AC为直径的两个半圆形区域,且看台Ⅰ的面积是看台Ⅱ的面积的3倍,矩形表演台BCDE 中,CD=10米,三角形水域ABC的面积为$400\sqrt{3}$平方米,设∠BAC=θ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4+2$\sqrt{3}$ | B. | 4-2$\sqrt{3}$ | C. | $\sqrt{3}$-1 | D. | $\sqrt{3}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
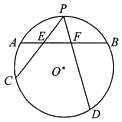 如图,已知AB为圆O的一条弦,点P为弧$\widehat{AB}$的中点,过点P任作两条弦PC,PD分别交AB于点E,F
如图,已知AB为圆O的一条弦,点P为弧$\widehat{AB}$的中点,过点P任作两条弦PC,PD分别交AB于点E,F查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<2} | B. | {x|1≤x<2} | C. | {x|1<x≤2} | D. | {x|1≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 观看 | 未观看 | 合计 | |
| 女生 | |||
| 男生 | |||
| 合计 | 50 |
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com