
���� ��1��L��x��=16$��4-\frac{3}{x+1}��$-x-2x=64-$\frac{48}{x+1}$-3x��0��x��5��������λ��Ԫ����
��2����һ��L��x��=67-$��\frac{48}{x+1}+3��x+1����$���û�������ʽ�����ʼ��ɵó����ֵ��
������L�䣨x��=$\frac{48}{��x+1��^{2}}$-3=$\frac{-3��x+5����x-3��}{��x+1��^{2}}$���L�䣨x��=0�����x=3�����ö����о������ĵ����Լ��ɵó�����ֵ�����ֵ
��� �⣺��1��L��x��=16$��4-\frac{3}{x+1}��$-x-2x=64-$\frac{48}{x+1}$-3x��0��x��5��������λ��Ԫ����
��2����һ��L��x��=67-$��\frac{48}{x+1}+3��x+1����$��67-$2��3��\sqrt{\frac{16}{x+1}����x+1��}$=43�����ҽ���x=3ʱȡ�Ⱥţ�
�൱Ͷ��ķ��Ϸ���Ϊ300Ԫʱ����ˮ��������õ�����������������4300Ԫ��
������L�䣨x��=$\frac{48}{��x+1��^{2}}$-3=$\frac{-3��x+5����x-3��}{��x+1��^{2}}$���L�䣨x��=0�����x=3��
�ɵ�x�ʣ�0��3��ʱ��L�䣨x����0������L��x������������x�ʣ�3��5]ʱ��L�䣨x����0������L��x�������ݼ���
�൱x=3ʱ������L��x��ȡ�ü���ֵ�����ֵ��
�൱Ͷ��ķ��Ϸ���Ϊ300Ԫʱ����ˮ��������õ�����������������4300Ԫ��
���� ���⿼�������õ����о������ļ�ֵ����ֵ��������Ӧ�á���������ʽ�����ʣ�������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|-2��x��1} | B�� | {x|x��2} | C�� | {0��1} | D�� | {1��2} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{5}}}{10}$ | B�� | $\frac{{\sqrt{5}}}{5}$ | C�� | $\frac{{2\sqrt{5}}}{5}$ | D�� | $\frac{{4\sqrt{5}}}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
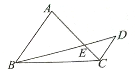 ��ͼ��ʾ��AC��BD���ڵ�E��AB��CD��AC=3$\sqrt{5}$��AB=2CD=6����tanA=2ʱ��$\overrightarrow{BE}•\overrightarrow{DC}$=-12��
��ͼ��ʾ��AC��BD���ڵ�E��AB��CD��AC=3$\sqrt{5}$��AB=2CD=6����tanA=2ʱ��$\overrightarrow{BE}•\overrightarrow{DC}$=-12���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com