
分析 (1)由c=1,e=$\frac{c}{a}$=$\frac{{\sqrt{2}}}{2}$,b2=a2-c2,求得a和b的值,求得椭圆方程;
(2)由题意可知设直线方程,将直线方程代入椭圆方程,由韦达定理可知求得y1+y2,y1•y2,由$\overrightarrow{AF}=λ\overrightarrow{FB}$(其中1<λ<3),可知:y1=-λy2,构造辅助函数t=λ+$\frac{1}{λ}$-2,t∈(0,3),代入求得m2=$\frac{2t}{4-t}$,根据向量数量积的坐标表示求得$\overrightarrow{OA}•\overrightarrow{OB}$=$\frac{1-2{m}^{2}}{2+{m}^{2}}$,m2=$\frac{2t}{4-t}$,根据一次函数的单调性即可求得$\overrightarrow{OA}•\overrightarrow{OB}$的取值范围.
解答 解:(1)由题意可知:设椭圆方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
c=1,椭圆的离心率e=$\frac{c}{a}$=$\frac{{\sqrt{2}}}{2}$,
∴a=$\sqrt{2}$,
由b2=a2-c2=1,
∴椭圆的方程为:$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)$\overrightarrow{AF}=λ\overrightarrow{FB}$(其中1<λ<3),可知直线斜率不为0,
设直线l:x=my-1,A(x1,y1),B(x2,y2),
∴y1=-λy2,
$\left\{\begin{array}{l}{x=my-1}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,整理得:(2+m2)y2-2my-1=0,
由韦达定理可知:y1+y2=$\frac{2m}{2+{m}^{2}}$,y1•y2=$\frac{-1}{2+{m}^{2}}$,
∴$\frac{4{m}^{2}}{2+{m}^{2}}$=$\frac{(1-λ)^{2}}{λ}$=λ+$\frac{1}{λ}$-2,
令t=λ+$\frac{1}{λ}$-2,t∈(0,$\frac{4}{3}$),
可得:m2=$\frac{2t}{4-t}$,
$\overrightarrow{OA}•\overrightarrow{OB}$=x1•x2+y1•y2=(my1-1)(my2-1)+y1•y2,
=(1+m2)y1•y2-m(y1+y2)+1,
=$\frac{1-2{m}^{2}}{2+{m}^{2}}$,
将m2=$\frac{2t}{4-t}$代入整理得:$\overrightarrow{OA}•\overrightarrow{OB}$=$\frac{4-5t}{8}$,t∈(0,$\frac{4}{3}$),
由f(t)=$\frac{4-5t}{8}$,在(0,$\frac{4}{3}$)单调递减,
∴$\overrightarrow{OA}•\overrightarrow{OB}$∈(-$\frac{1}{3}$,$\frac{1}{2}$).
点评 本题考查椭圆的方程及简单几何性质,考查直线与椭圆的位置关系,韦达定理向量数量积的坐标运算,函数的最值,考查构造法,考查计算能力,属于中档题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{5}$ | B. | $\frac{12}{5}$ | C. | $\frac{18}{5}$ | D. | $\frac{24}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
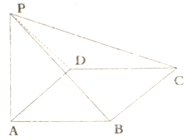 四棱锥P-ABCD的底面是菱形,∠BAD=60°,PA⊥底面ABCD,PA=AB=a,E为棱PC上点.
四棱锥P-ABCD的底面是菱形,∠BAD=60°,PA⊥底面ABCD,PA=AB=a,E为棱PC上点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com