
分析 由双曲线的标准方程可知:则x=2secα,y=tanα,由3x2-2xy=12sec2α-4secαtanα=$\frac{4}{1-sinα}$+$\frac{8}{1+sinα}$,由-1<sinα<1,1-sinα>0,1+sinα>0,由基本不等式的性质可知∴[(1-sinα)+(1+sinα)]•($\frac{4}{1-sinα}$+$\frac{8}{1+sinα}$)≥12+2$\sqrt{\frac{4(1+sinα)}{1-sinα}×\frac{8(1-sinα)}{1+sinα}}$=12+8$\sqrt{2}$,则$\frac{4}{1-sinα}$+$\frac{8}{1+sinα}$≥6+4$\sqrt{2}$,即可求得3x2-2xy的最小值.
解答 解:由线$\frac{{x}^{2}}{4}$-y2=1,设x=2secα,y=tanα,
3x2-2xy=12sec2α-4secαtanα,
=$\frac{12}{co{s}^{2}α}$-$\frac{4sinα}{co{s}^{2}α}$,
=$\frac{12-4sinα}{co{s}^{2}α}$
=$\frac{12-4sinα}{1-si{n}^{2}α}$,
=$\frac{4}{1-sinα}$+$\frac{8}{1+sinα}$
∵-1<sinα<1,
1-sinα>0,1+sinα>0
∴[(1-sinα)+(1+sinα)]•($\frac{4}{1-sinα}$+$\frac{8}{1+sinα}$),
=12+$\frac{4(1+sinα)}{1-sinα}$+$\frac{8(1-sinα)}{1+sinα}$≥12+2$\sqrt{\frac{4(1+sinα)}{1-sinα}×\frac{8(1-sinα)}{1+sinα}}$=12+8$\sqrt{2}$,
当且仅当$\frac{4(1+sinα)}{1-sinα}$=$\frac{8(1-sinα)}{1+sinα}$等号成立,
解得:sinα=3-2$\sqrt{2}$(3+2$\sqrt{2}$舍去)时,取得最小值,
∵[(1-sinα)+(1+sinα)]•($\frac{4}{1-sinα}$+$\frac{8}{1+sinα}$)=2($\frac{4}{1-sinα}$+$\frac{8}{1+sinα}$),
$\frac{4}{1-sinα}$+$\frac{8}{1+sinα}$≥6+4$\sqrt{2}$,
∴3x2-2xy的最小值是6+4$\sqrt{2}$,
故答案为:6+4$\sqrt{2}$.
点评 本题考查双曲线的参数方程,三角恒等变换,基本不等式性质的综合应用,考查计算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
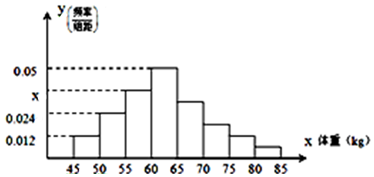
| A. | 0.044 | B. | 0.039 | C. | 0.01 | D. | 0.04 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A=B | B. | A∩B=∅ | C. | A∩B=A | D. | A∪B=A |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com