练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形
    （Ⅰ）求椭圆C的标准方程；
    （Ⅱ）设F为椭圆C的左焦点，M为直线x=-3上任意一点，过F作MF的垂线交椭圆C于点P，Q
    （i）证明：OM平分线段PQ（其中O为坐标原点）；
    （ii）当$\frac{|MF|}{|PQ|}$最小时，求点M的坐标．

    分析 （I）由椭圆C的焦距为4，及等边三角形的性质和a2=b2+c2，求得a，b，即可求椭圆C的标准方程；
    （Ⅱ）（i）设M（-3，m），P（x1，y1），Q（x2，y2），PQ的中点为N（x0，y0），kMF=-m，设直线PQ的方程为x=my-2，代入椭圆方程，运用韦达定理和中点坐标公式，结合三点共线的方法：斜率相等，即可得证；
    （ii）利用两点间距离公式及弦长公式将$\frac{|MF|}{|PQ|}$表示出来，由换元法和基本不等式，可得$\frac{|MF|}{|PQ|}$取最小值时的条件获得等量关系，从而确定点M的坐标．

    解答 解：（Ⅰ）由题意可得c=2，
    短轴的两个端点与长轴的一个端点构成正三角形，可得
    a=$\frac{\sqrt{3}}{2}$•2b，即有a=$\sqrt{3}$b，a2-b2=4，
    解得a=$\sqrt{6}$，b=$\sqrt{2}$，
    则椭圆方程为$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1；
    （Ⅱ）设M（-3，m），P（x1，y1），Q（x2，y2），
    PQ的中点为N（x0，y0），kMF=-m，
    （i）证明：由F（-2，0），可设直线PQ的方程为x=my-2，
    代入椭圆方程可得（m2+3）y2-4my-2=0，
    ∴y1+y2=$\frac{4m}{3+{m}^{2}}$，y1y2=-$\frac{2}{3+{m}^{2}}$，
    于是N（-$\frac{6}{3+{m}^{2}}$，$\frac{2m}{3+{m}^{2}}$），
    则直线ON的斜率kON=-$\frac{m}{3}$，
    又kOM=-$\frac{m}{3}$，
    ∴kOM=kON，
    ∴O，N，M三点共线，即有OM平分线段PQ；
    （ii）由两点间距离公式得|MF|=$\sqrt{1+{m}^{2}}$，
    由弦长公式得|PQ|=$\sqrt{1+{m}^{2}}$•|y1-y2|
    =$\sqrt{1+{m}^{2}}$•$\sqrt{（{y}_{1}+{y}_{2}）^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{1+{m}^{2}}$•$\frac{\sqrt{24（{m}^{2}+1）}}{3+{m}^{2}}$，
    ∴$\frac{|MF|}{|PQ|}$=$\frac{3+{m}^{2}}{2\sqrt{6}•\sqrt{1+{m}^{2}}}$，
    令t=$\sqrt{1+{m}^{2}}$（t≥1），
    则$\frac{|MF|}{|PQ|}$=$\frac{{t}^{2}+2}{2\sqrt{6}t}$=$\frac{1}{2\sqrt{6}}$（t+$\frac{2}{t}$）≥$\frac{1}{2\sqrt{6}}$•2$\sqrt{2}$=$\frac{\sqrt{3}}{3}$（当且仅当t2=2时，取“=”号），
    ∴当$\frac{|MF|}{|PQ|}$最小时，由t2=2=m2+1，得m=1或m=-1，
    此时点M的坐标为（-3，1）或（-3，-1）．

    点评 本题考查椭圆的方程和性质，主要考查椭圆方程的运用，注意联立直线方程，运用韦达定理和中点坐标公式，同时考查弦长公式和基本不等式的运用，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    11．已知直角坐标系中动点P（1+cosα，sinα）参数α∈[0，2π]，在以原点为极点，x轴正半轴为极轴所建立的极坐标系中，动点Q（ρ，θ）在曲线C：$\frac{sinθ}{a}$-cosθ=$\frac{1}{ρ}$上
    （1）在直角坐标系中，求点P的轨迹E的方程和曲线C的方程
    （2）若动点P的轨迹E和曲线C有两个公共点，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．设a＞b＞0，则下列不等式恒成立的为（　　）
    A．$\frac{1}{a}$＞$\frac{1}{b}$B．ac＞bcC．$\sqrt{a}$＞$\sqrt{b}$D．$\frac{a}{c}$＞$\frac{b}{c}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．“x≠1“是“x＜1”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既非充分也分必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．某几何体的三视图如图所示，则该几何体的表面积为（　　）
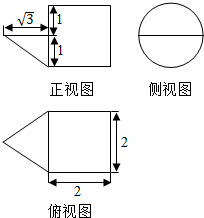
    A．$\frac{13π}{2}+\sqrt{3}$B．$\frac{（12+\sqrt{3}）π}{6}$C．$\frac{15π}{2}$D．$\frac{（6+\sqrt{3}）π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．在△ABC中，A、B、C的对边分别为a、b、c，已知a=$\sqrt{3}$，且4sin2$\frac{B+C}{2}$-cos2A=$\frac{7}{2}$．
    （1）求角A的大小；          
    （2）求△ABC的周长l取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知命题p：若x∈N*，则x∈Z．命题q：?x0∈R，${（\frac{1}{2}）^{x_0}}=0$．则下列命题为真命题的是（　　）
    A．￢pB．p∧qC．￢p∨qD．￢p∨￢q

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．设函数f（x）=$\overrightarrow{a}•\overrightarrow{b}$，其中向量$\overrightarrow{a}$=（m，cos2x），$\overrightarrow{b}$=（1+sin2x，1），且y=f（x）的图象经过点$（{\frac{π}{4}，2}）$，则实数m的值为（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    同步练习册答案