
分析 (1)由题意$\overline{P{F}_{1}}$•$\overline{P{F}_{2}}$的最大值是1,可得a2-c2=1,即b=1,利用$\overline{P{F}_{1}}$•$\overline{P{F}_{2}}$的是最小值是-$\frac{11}{5}$解得b,即可求椭圆方程.
(2)设直线AS的斜率为k>0,利用kAS•kBS=-$\frac{{b}^{2}}{{a}^{2}}$=-$\frac{1}{4}$,可得kBS=-$\frac{1}{4k}$.直线AS,BS的方程分别为:y=k(x+2),y=-$\frac{1}{4k}$(x-2).令x=$\frac{34}{15}$,可得M,N.求出|MN|再利用基本不等式的性质即可得出.
解答  解:(1)由题意$\overline{P{F}_{1}}$•$\overline{P{F}_{2}}$的最大值是1,可得a2-c2=1,即b=1,
解:(1)由题意$\overline{P{F}_{1}}$•$\overline{P{F}_{2}}$的最大值是1,可得a2-c2=1,即b=1,
∴AD的方程为y=$\frac{x}{a}$+1
设P(x,y)(-a≤x≤0),则
$\overline{P{F}_{1}}$•$\overline{P{F}_{2}}$=(x+c,y)•(x-c,y)=x2-c2+y2=
(1+$\frac{1}{{a}^{2}}$)(x+$\frac{a}{{a}^{2}+1}$)2-$\frac{{a}^{4}-{a}^{2}-1}{{a}^{2}+1}$
∵$\overline{P{F}_{1}}$•$\overline{P{F}_{2}}$的最小值是-$\frac{11}{5}$.
∴-$\frac{{a}^{4}-{a}^{2}-1}{{a}^{2}+1}$=-$\frac{11}{5}$
∴a2=4,b=1,
所求的椭圆的方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$.
(2)设直线AS的斜率为k>0,
∵kAS•kBS=-$\frac{{b}^{2}}{{a}^{2}}$=-$\frac{1}{4}$,
∴kBS=-$\frac{1}{4k}$.
∴直线AS,BS的方程分别为:y=k(x+2),y=-$\frac{1}{4k}$(x-2).
令x=$\frac{34}{15}$,则M($\frac{34}{15}$,$\frac{64k}{15}$),N($\frac{34}{15}$,-$\frac{1}{15k}$).
∴|MN|=$\frac{64k}{15}+\frac{1}{15k}$≥$\frac{1}{15}×2\sqrt{64k•\frac{1}{k}}$=$\frac{16}{15}$,当且仅当k=$\frac{1}{8}$时取等号.
∴线段MN长度的最小值为$\frac{16}{15}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、基本不等式的性质,考查了推理能力与计算能力,属于中档题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
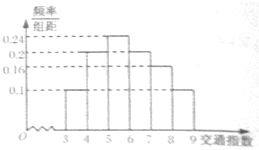 交通指数是交通拥堵指数的简称,是综合反映道路间畅通或拥堵的概念.记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从郑州市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图 所示:
交通指数是交通拥堵指数的简称,是综合反映道路间畅通或拥堵的概念.记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从郑州市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图 所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 720 | B. | 270 | C. | 390 | D. | 300 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图1在直角三角形ABC中,∠A=90°,AB=2,AC=4,D,E分别是AC,BC边上的中点,M为CD的中点,现将△CDE沿DE折起,使点A在平面CDE内的射影恰好为M.
如图1在直角三角形ABC中,∠A=90°,AB=2,AC=4,D,E分别是AC,BC边上的中点,M为CD的中点,现将△CDE沿DE折起,使点A在平面CDE内的射影恰好为M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com