
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过
,过![]() 的左焦点
的左焦点![]() 的直线
的直线![]() ,直线
,直线![]() 被圆
被圆![]() :
:![]() 截得的弦长为
截得的弦长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 的右焦点为
的右焦点为![]() ,在圆
,在圆![]() 上是否存在点
上是否存在点![]() ,满足
,满足![]() ,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.
,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】我市两所高中分别组织部分学生参加了“七五普法网络知识大赛”,现从这两所学校的参赛学生中分别随机抽取30名学生的成绩(百分制)作为样本,得到样本数据的茎叶图如图所示.
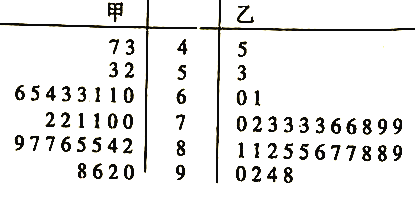
(Ⅰ)若乙校每位学生被抽取的概率为0.15,求乙校参赛学生总人数;
(Ⅱ)根据茎叶图,从平均水平与波动情况两个方面分析甲、乙两校参赛学生成绩(不要求计算);
(Ⅲ)从样本成绩低于60分的学生中随机抽取3人,求3人不在同一学校的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x2﹣1)=loga ![]() (a>0且a≠1)
(a>0且a≠1)
(1)求函数f(x)的解析式,并判断f(x)的奇偶性;
(2)解关于x的方程f(x)=loga ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,已知中心在原点,焦点在x轴上的双曲线C的离心率为![]() ,且双曲线C与斜率为2的直线l相交,且其中一个交点为P(﹣3,0).
,且双曲线C与斜率为2的直线l相交,且其中一个交点为P(﹣3,0).
(1)求双曲线C的方程及它的渐近线方程;
(2)求以直线l与坐标轴的交点为焦点的抛物线的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数,
为参数,![]() ),其中
),其中![]() ,在以
,在以![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() ,曲线
,曲线![]() .
.
(Ⅰ)求![]() 与
与![]() 交点的直角坐标系;
交点的直角坐标系;
(Ⅱ)若![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】血药浓度(Plasma Concentration)是指药物吸收后在血浆内的总浓度. 药物在人体内发挥治疗作用时,该药物的血药浓度应介于最低有效浓度和最低中毒浓度之间.已知成人单次服用1单位某药物后,体内血药浓度及相关信息如图所示:
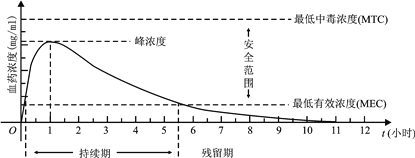
根据图中提供的信息,下列关于成人使用该药物的说法中,不正确的个数是
①首次服用该药物1单位约10分钟后,药物发挥治疗作用
②每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒
③每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用
④首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x),对任意a,b∈R,都有f(a+b)=f(a)+f(b)﹣1,当x>0时,f(x)>1;且f(2)=3,
(1)求f(0)及f(1)的值;
(2)判断函数f(x)在R上的单调性,并给予证明;
(3)若f(﹣kx2)+f(kx﹣2)<2对任意的x∈R恒成立,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com