
现有甲、乙两个靶。某射手向甲靶射击一次,命中的概率为 ,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为 ,每命中一次得2分,没有命中得0分。该射手每次射击的结果相互独立。假设该射手完成以上三次射击。
,每命中一次得2分,没有命中得0分。该射手每次射击的结果相互独立。假设该射手完成以上三次射击。
(Ⅰ)求该射手恰好命中一次的概率;
(Ⅱ)求该射手的总得分X的分布列及数学期望EX.
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:解答题
哈尔滨市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的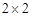 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为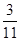 。
。
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 110 |
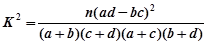 。
。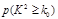 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
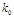 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人在罚球线互不影响地投球,命中的概率分别为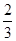 与
与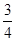 ,投中得1分,投不中得0分.
,投中得1分,投不中得0分.
(1)甲、乙两人在罚球线各投球一次,求两人得分之和 的数学期望;
的数学期望;
(2)甲、乙两人在罚球线各投球二次,求甲恰好比乙多得分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了保养汽车,维护汽车性能,汽车保养一般都在购车的4S店进行,某地大众汽车4S店售后服务部设有一个服务窗口专门接待保养预约。假设车主预约保养登记所需的时间互相独立,且都是整数分钟,对以往车主预约登记所需的时间统计结果如下:
| 登记所需时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲有一个箱子,里面放有x个红球,y个白球(x,y≥0,且x+y=4);乙有一个箱子,里面放有2个红球,1个白球,1个黄球.现在甲从箱子里任取2个球,乙从箱子里任取1个球.若取出的3个球颜色全不相同,则甲获胜.
(1)试问甲如何安排箱子里两种颜色球的个数,才能使自己获胜的概率最大?
(2)在(1)的条件下,求取出的3个球中红球个数的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
从编号为1,2,3,4,5的五个形状大小相同的球中,任取2个球,求:(1)取到的这2个球编号之和为5的概率;(2)取到的这2个球编号之和为奇数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人独立地破译1个密码, 他们能译出密码的概率分别为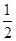 和
和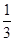 , 求:
, 求:
(1)甲、乙两人至少有一个人破译出密码的概率;
(2)两人都没有破译出密码的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
甲,乙,丙三位学生独立地解同一道题,甲做对的概率为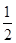 ,乙,丙做对的概率分别为
,乙,丙做对的概率分别为 ,
, (
( >
> ),且三位学生是否做对相互独立.记
),且三位学生是否做对相互独立.记 为这三位学生中做对该题的人数,其分布列为:
为这三位学生中做对该题的人数,其分布列为:
 | 0 | 1 | 2 | 3 |
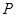 | 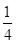 |  | 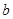 | 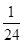 |
 ,
, 的值;
的值; 的数学期望.
的数学期望. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com