
| 员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 年薪(万元) | 3 | 3.5 | 4 | 5 | 5.5 | 6.5 | 7 | 7.5 | 8 | 50 |
分析 (1)根据表格数据计算;
(2)适用组合数公式计算P(ξ);
(3)求出线性回归方程,根据回归方程预测.
解答 解:(1)平均值为10万元,中位数为6万元.
(2)年薪高于5万的有6人,低于或等于5万的有4人;ξ的取值为0,1,2.P(ξ=0)$\frac{{C}_{4}^{2}}{{C}_{10}^{2}}$=$\frac{2}{15}$,$P(ξ=1)=\frac{C_4^1C_6^1}{{C_{10}^2}}=\frac{8}{15}$,$P(ξ=2)=\frac{C_6^2}{{C_{10}^2}}=\frac{1}{3}$,
所以ξ的分布列为
| ξ | 0 | 1 | 2 |
| P | $\frac{2}{15}$ | $\frac{8}{15}$ | $\frac{1}{3}$ |
点评 本题考查了古典概型的概率计算,线性回归方程的解法及应用,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,正方体ABCD-A1B1C1D1中,P是AD的中点.
如图,正方体ABCD-A1B1C1D1中,P是AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{7}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 3 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
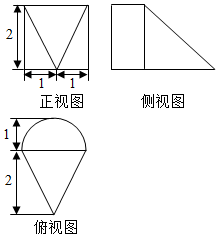
| A. | $π+\frac{8}{3}$ | B. | $\frac{π}{3}+\frac{8}{3}$ | C. | π+8 | D. | $\frac{π}{2}+\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com