
已知对称中心为坐标原点的椭圆C1与抛物线C2:x2=4y有一个相同的焦点F1,直线l:y=2x+m与抛物线C2只有一个公共点.
(1)求直线l的方程;
(2)若椭圆C1经过直线l上的点P,当椭圆C1的离心率取得最大值时,求椭圆C1的方程及点P的坐标.
解 (1)由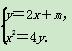 消去y,得x2-8x-4m=0,
消去y,得x2-8x-4m=0,
∵直线l与抛物线C2只有一个公共点,
∴Δ=82+4×4m=0,解得m=-4.
∴直线l的方程为y=2x-4.
(2)∵抛物线C2的焦点为F1(0,1),依题意知椭圆C1的两个焦点的坐标为F1(0,1),F2(0,-1)
设椭圆C1的方程为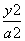 +
+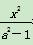 =1(a>1),
=1(a>1),
由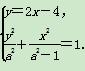 消去y,得(5a2-4)x2-16(a2-1)x+(a2-1)(16-a2)=0.(*)
消去y,得(5a2-4)x2-16(a2-1)x+(a2-1)(16-a2)=0.(*)
由Δ=162(a2-1)2-4(5a2-4)(a2-1)(16-a2)≥0,得a4-4a2≥0(a2>0且a2-1>0),解得a2≥4.∵a>1,∴a≥2,∴e= ≤
≤ .
.
当a=2时,emax= ,此时椭圆C1的方程为
,此时椭圆C1的方程为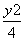 +
+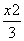 =1.
=1.
把a=2代入方程(*),解得x=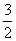 .
.
又y=2x-4,∴y=-1,
∴点P的坐标为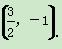 .
.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
已知△ABP的三个顶点都在抛物线C:x2=4y上,F为抛物线C的焦点,点M为AB的中点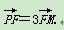
(1)若|PF|=3,求点M的坐标;
(2)求△ABP面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
某地有居民100 000户,其中普通家庭99 000户,高收入家庭1 000户.从普通家庭中以简单随机抽样方式抽取990户,从高收入家庭中以简单随机抽样方式抽取100户进行调查,发现共有120户家庭拥有3套或3套以上住房,其中普通家庭50户,高收入家庭70户.依据这些数据并结合所掌握的统计知识,你认为该地拥有3套或3套以上住房的家庭所占比例的合理估计是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
高三年级的三个班去甲、乙、丙、丁四个工厂参加社会实践,但去何工厂可自由选择,甲工厂必须有班级要去,则不同的分配方案有( )
A.16种 B.18种
C.37种 D.48种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com