练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    直线y＝kx＋2与抛物线y2＝8x有且只有一个公共点，则k的值为(　　)

    A．1                                    B．1或3

    C．0                                    D．1或0

     


    　D

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    动圆C经过点F(1,0)，并且与直线x＝－1相切，若动圆C与直线y＝x＋2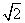＋1总有公共点，则圆C的面积(　　)

    A．有最大值8π                          B．有最小值2π

    C．有最小值3π                          D．有最小值4π

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点A(－2,3)在抛物线C：y2＝2px的准线上，记C的焦点为F，则直线AF的斜率为(　　)

    A．－                                 B．－1

    C．－                                 D．－

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知F1，F2分别为椭圆C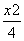：＋＝1的左、右焦点，点P为椭圆C上的动点，则△PF1F2的重心G的轨迹方程为(　　)

    A.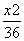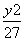＋＝1(y≠0)　　                B.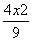＋y2＝1(y≠0)

    C.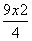＋3y2＝1(y≠0)　　                D．x2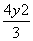＋＝1(y≠0)

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在Rt△ABC中，∠CAB＝90°，AB＝2，AC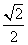＝，一曲线E过C点，动点P在曲线E上运动，且保持|PA|＋|PB|的值不变．

    (1)建立适当的坐标系，求曲线E的方程；

    (2)直线l：y＝x＋t与曲线E交于M，N两点，求四边形MANB的面积的最大值．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    与抛物线y2＝8x相切、倾斜角为135°的直线l与x轴和y轴的交点分别是A，B，那么过A，B两点的最小圆截抛物线y2＝8x的准线所得的弦长为(　　)

    A．4                                    B．2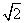

    C．2                                    D.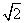

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知对称中心为坐标原点的椭圆C1与抛物线C2：x2＝4y有一个相同的焦点F1，直线l：y＝2x＋m与抛物线C2只有一个公共点．

    (1)求直线l的方程；

    (2)若椭圆C1经过直线l上的点P，当椭圆C1的离心率取得最大值时，求椭圆C1的方程及点P的坐标．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    执行如图所示的程序框图，如果输入a＝2，b＝2，那么输出的a值为(　　)

    A．4                                    B．16

    C．256                                  D．log316

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某车间为了规定工时定额．需要确定加工零件所需时间，为此进行了5次试验，收集到如下数据，由最小二乘法求得回归直线方程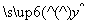＝0.67x＋54.9.

    零件数x(个)

    10

    20

    30

    40

    50

    加工时间y(min)

    6       2

     

    75

    81

    89

    后来表中一个数据模糊不清了，请你推断出该数据为________．

     

    查看答案和解析>>

    同步练习册答案