已知角α的顶点在原点，始边与x轴的正半轴重合，终边经过点P(－3，
)．
(1)求sin 2α－tan α的值；
(2)若函数f(x)＝cos(x－α)cos α－sin(x－α)sin α，求函数y＝f
－2f2(x)在区间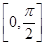
上的值域．
每课必练系列答案科目：高中数学 来源： 题型：解答题
已知函数f(x)＝sin(ωx＋φ)(ω>0，|φ|<π)的部分图像如图所示，
(1)求ω，φ的值；
(2)设g(x)＝2
f
f
－1，当x∈[0，
]时，求函数g(x)的值域．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知a>0,函数f(x)=-2asin(2x+
)+2a+b,当x∈[0,
]时,-5≤f(x)≤1.
(1)求常数a,b的值.
(2)设g(x)=f(x+)且lg g(x)>0,求g(x)的单调区间.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数
（
）的最小正周期为
．
（1）求函数
的单调增区间；
（2）将函数的图象向左平移
个单位，再向上平移
个单位，得到函数
的图象．若在
上至少含有
个零点，求
的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
如图，某园林单位准备绿化一块直径为BC的半圆形空地，△ABC外的地方种草，△ABC的内接正方形PQRS为一水池，其余的地方种花，若BC＝a，∠ABC＝θ，设△ABC的面积为S1，正方形的PQRS面积为S2.
(1)用a，θ表示S1和S2；
(2)当a固定，θ变化时，求
的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积所用的经验公式为：弧田面积=
（弦´矢+矢2）.弧田（如图），由圆弧和其所对弦所围成，公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差.
按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为
，弦长等于9米的弧田.
（1）计算弧田的实际面积；
（2）按照《九章算术》中弧田面积的经验公式计算所得结果与（1）中计算的弧田实际面积相差多少平方米？（结果保留两位小数）
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数f(x)＝2sin
(0≤x≤5)，点A、B分别是函数y＝f(x)图象上的最高点和最低点．
(1)求点A、B的坐标以及
·
的值；
(2)设点A、B分别在角α、β的终边上，求tan(α－2β)的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
(2) [－2,1]
(x∈R)的图象，只需把函数y＝2sinx(x∈R)的图象上所有的点经过怎样的变换得到？
的最小正周期及在区间
上的最大值和最小值；
，求
的值.