
已知函数 (
( )的最小正周期为
)的最小正周期为 .
.
(1)求函数 的单调增区间;
的单调增区间;
(2)将函数 的图象向左平移
的图象向左平移 个单位,再向上平移
个单位,再向上平移 个单位,得到函数
个单位,得到函数 的图象.若
的图象.若 在
在 上至少含有
上至少含有 个零点,求
个零点,求 的最小值.
的最小值.
(1)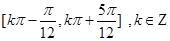 (2)
(2)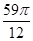
解析试题分析:
(1)要求单调区间,首先要对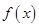 进行化简得到最间形式,依次利用正弦二倍角,降幂公式,和辅助角公式就可以得到
进行化简得到最间形式,依次利用正弦二倍角,降幂公式,和辅助角公式就可以得到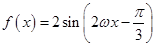 ,进而利用复合函数的单调性内外结合求得函数
,进而利用复合函数的单调性内外结合求得函数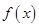 的单调区间.
的单调区间.
(2)利用“左加右减,上加下减”得到平移后的函数解析式 ,令
,令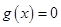 ,求出所有的零点,在根据
,求出所有的零点,在根据 上至少含有
上至少含有 个零点,得到b的取值范围,进而得到b的最小值.
个零点,得到b的取值范围,进而得到b的最小值.
试题解析:
(1)由题意得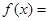
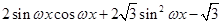
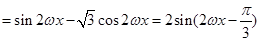 2分
2分
由周期为 ,得
,得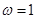 .得
.得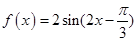 4分
4分
由正弦函数的单调增区间得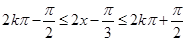 ,得
,得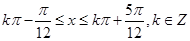
所以函数 的单调增区间是
的单调增区间是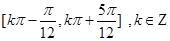 6分
6分
(2)将函数 的图象向左平移
的图象向左平移 个单位,再向上平移1个单位,
个单位,再向上平移1个单位,
得到 的图象,所以
的图象,所以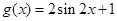 8分
8分
令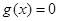 ,得:
,得: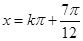 或
或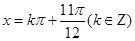 10分
10分
所以在每个周期上恰好有两个零点,若 在
在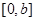 上有
上有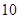 个零点,
个零点,
则 不小于第
不小于第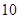 个零点的横坐标即可,即
个零点的横坐标即可,即 的最小值为
的最小值为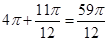 12分
12分
考点:零点 单调性 辅助角公式 正余弦倍角公式


科目:高中数学 来源: 题型:解答题
已知角α的顶点在原点,始边与x轴的正半轴重合,终边经过点P(-3, ).
).
(1)求sin 2α-tan α的值;
(2)若函数f(x)=cos(x-α)cos α-sin(x-α)sin α,求函数y= f
f -2f2(x)在区间
-2f2(x)在区间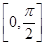 上的值域.
上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
函数f(x)=sin(ωx+φ)ω>0,|φ|< 的部分图像如图Z3-4所示,将y=f(x)的图像向右平移
的部分图像如图Z3-4所示,将y=f(x)的图像向右平移 个单位长度后得到函数y=g(x)的图像.
个单位长度后得到函数y=g(x)的图像.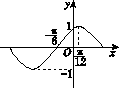
(1)求函数y=g(x)的解析式;
(2)在△ABC中,它的三个内角满足2sin2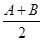 =gC+
=gC+ +1,且其外接圆半径R=2,求△ABC的面积的最大值.
+1,且其外接圆半径R=2,求△ABC的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com