
【题目】某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路和山区边界的直线型公路,记两条相互垂直的公路为l1,l2,山区边界曲线为C,计划修建的公路为l,如图所示,M,N为C的两个端点,测得点M到l1,l2的距离分别为5千米和40千米,点N到l1,l2的距离分别为20千米和2.5千米,以l2,l1所在的直线分别为x,y轴,建立平面直角坐标系xOy,假设曲线C符合函数y=![]() (其中a,b为常数)模型.
(其中a,b为常数)模型.
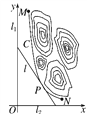
(1)求a,b的值;
(2)设公路l与曲线C相切于P点,P的横坐标为t.
①请写出公路l长度的函数解析式f(t),并写出其定义域;
②当t为何值时,公路l的长度最短?求出最短长度.
【答案】(1) 见解析(2)见解析
【解析】试题分析:(1)由题意知,点M,N的坐标分别为(5,40),(20,2.5),将其分别代入y=![]() 建立方程组,即可求a,b的值;(2)①求出切线l的方程,可得A,B的坐标,即可写出公路l长度的函数解析式f(t),并写出其定义域;②设g(t)=t2+
建立方程组,即可求a,b的值;(2)①求出切线l的方程,可得A,B的坐标,即可写出公路l长度的函数解析式f(t),并写出其定义域;②设g(t)=t2+![]() 利用导数,确定单调性,即可求出当t为何值时,公路l的长度最短,并求出最短长度.
利用导数,确定单调性,即可求出当t为何值时,公路l的长度最短,并求出最短长度.
试题解析:
(1)由题意知,点M,N的坐标分别为(5,40),(20,2.5).
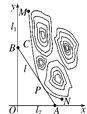
将其分别代入y=![]() ,
,
得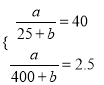 解得
解得![]() ,
,
(2)①由(1)知,y=![]() (5≤x≤20),
(5≤x≤20),
则点P的坐标为![]() ,设在点P处的切线l交x,
,设在点P处的切线l交x,
y轴分别于A,B点,y′=-![]() ,
,
则l的方程为
y-![]() =-
=-![]() (x-t),
(x-t),
由此得A![]() ,B
,B![]() .
.
故f(t)=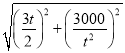 =
=![]()
![]() ,t∈[5,20].
,t∈[5,20].
②设g(t)=t2+![]() ,则g′(t)=2t-
,则g′(t)=2t-![]() .
.
令g′(t)=0,解得t=10![]() .
.
当t∈(5,10![]() )时,g′(t)<0,g(t)是减函数;
)时,g′(t)<0,g(t)是减函数;
当t∈(10![]() ,20)时,g′(t)>0,g(t)是增函数.
,20)时,g′(t)>0,g(t)是增函数.
从而,当t=10![]() 时,函数g(t)有极小值,也是最小值,
时,函数g(t)有极小值,也是最小值,
所以g(t)min=300,此时f(t)min=15![]() .
.
答 当t=10![]() 时,公路l的长度最短,最短长度为15
时,公路l的长度最短,最短长度为15![]() 千米.
千米.


科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线与半径
的垂直平分线与半径![]() 交于
交于![]() 点,当点
点,当点![]() 在圆
在圆![]() 上运动时,
上运动时,
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过![]() 作直线
作直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,
两点, ![]() 为坐标原点,求
为坐标原点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,设倾斜角为
中,设倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数)与曲线
为参数)与曲线 (
(![]() 为参数)相交于不同的两点
为参数)相交于不同的两点![]() 、
、![]() .
.
(1)若![]() ,求线段
,求线段![]() 的中点的直角坐标;
的中点的直角坐标;
(2)若直线![]() 的斜率为
的斜率为![]() ,且过已知点
,且过已知点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知在极坐标系和直角坐标系中,极点与直角坐标系的原点重合,极轴与![]() 轴的非负半轴重合,曲线
轴的非负半轴重合,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)判断曲线![]() 与曲线
与曲线![]() 的位置关系,若两曲线相交,求出两交点间的距离.
的位置关系,若两曲线相交,求出两交点间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin ωx-cos ωx(ω>0)的最小正周期为π.
(1)求函数y=f(x)图象的对称轴方程;
(2)讨论函数f(x)在![]() 上的单调性.
上的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区![]() 的年平均浓度不得超过3S微克/立方米,
的年平均浓度不得超过3S微克/立方米, ![]() 的24小时平均浓度不得超过75微克/立方米.某市环保局随机抽取了一居民区2016年20天
的24小时平均浓度不得超过75微克/立方米.某市环保局随机抽取了一居民区2016年20天![]() 的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如图表:
的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如图表:
组别 |
| 频数(天) | 频率 |
第一组 |
| 3 | 0.15 |
第二组 |
| 12 | 0.6 |
第三组 |
| 3 | 0.15 |
第四组 |
| 2 | 0.1 |
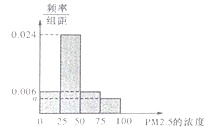
(Ⅰ)将这20天的测量结果按表中分组方法绘制成的样本频率分布直方图如图.
(ⅰ)求图中![]() 的值;
的值;
(ⅱ)在频率分布直方图中估算样本平均数,并根据样本估计总体的思想,从![]() 的年平均度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
的年平均度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
(Ⅱ)将频率视为概率,对于2016年的某3天,记这3天中该居民区![]() 的24小时平均浓度符合环境空气质量标准的天数为
的24小时平均浓度符合环境空气质量标准的天数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆G: ![]() 的离心率为
的离心率为![]() ,过椭圆G右焦点F的直线m:x=1与椭圆G交于点M(点M在第一象限).
,过椭圆G右焦点F的直线m:x=1与椭圆G交于点M(点M在第一象限).
(Ⅰ)求椭圆G的方程;
(Ⅱ)已知A为椭圆G的左顶点,平行于AM的直线l与椭圆G相交于B,C两点,请判断直线MB,MC是否关于直线m对称,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com