练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
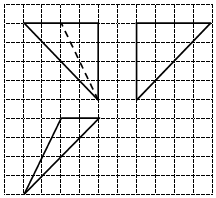
    13．如图，网格纸上小正方形的边长为1，粗实（虚）线画出的是某多面体的三视图，则该多面体的体积为（　　）
    A．64B．$\frac{64}{3}$C．16D．$\frac{16}{3}$

    分析 根据三视图知几何体是三棱锥、为棱长为4的正方体一部分，画出直观图，由正方体的性质判断出线面位置关系、求出底面的面积，由椎体的体积公式求出该多面体的体积．

    解答 解：根据三视图知几何体是：三棱锥D-ABC、为棱长为4的正方体一部分，
    直观图如图所示：B是棱的中点，
    由正方体的性质得，CD⊥平面ABC，
    △ABC的面积S=$\frac{1}{2}×2×4$=4，
    所以该多面体的体积V=$\frac{1}{3}×4×4$=$\frac{16}{3}$，
    故选：D．

    点评 本题考查三视图求几何体的体积，结合三视图和对应的正方体复原几何体是解题的关键，考查空间想象能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    3．已知定义域为R的奇函数f（x）的导函数f′（x），当x≠0时，f′（x）-$\frac{f（x）}{x}＞0$，若a=$\frac{f（cos3）}{cos3}$，b=-$\frac{f（-2016）}{2016}$，c=（log3e）f（ln3），则下列关于a、b、c的大小关系正确的是（　　）
    A．b＞c＞aB．a＞c＞bC．c＞b＞aD．b＞a＞c

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．命题p：?a∈（0，1）∪（1，+∞），函数f（x）=loga（x-1）的图象过点（2，0），命题q：?x∈N，x3＜x2．则（　　）
    A．p假q假B．p真q假C．p假q真D．p真q真

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知函数f（x）=$\frac{m}{x+1}$+nlnx（m，n为常数）的图象在x=1处的切线方程为x+y-2=0
    （1）判断函数f（x）的单调性；
    （2）已知p∈（0，1），且f（p）=2，若对任意x∈（p，1），任意t∈[$\frac{1}{2}$，2]，f（x）≥t3-t2-2at+2与f（x）≤t3-t2-2at+2中恰有一个恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．一台机器由于使用时间较长，但还可以使用，它按不同的转速生产出来的某机器零件有一些会有缺点，每小时生产有缺点零件的多少随机器运转的速度而变化，如表是抽样试验结果：
    转速x/（rad/s）1614128
    每小时生产有缺点的零件数y/件11985
    若实际生产中，允许每小时的产品中有缺点的零件数最多为10个，求机器的转速应该控制所在的范围．$\left\{{\begin{array}{l}{b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}}\\{a=\overline y-b\overline x}\end{array}}\right.$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，且底面ABCD为直角梯形，∠BAD=90°，AB∥DC．已知AD=DC=PA=1，AB=2．
    （Ⅰ） 求证：平面PAD⊥平面PCD；
    （Ⅱ） 设M为PB上的点，且PM=$\frac{1}{3}$PB，求证：PD∥平面ACM；
    （Ⅲ） 在（Ⅱ）的条件下，求二面角P-AC-M的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

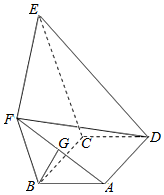    5．如图，四边形ABCD为矩形，四边形BCEF为直角梯形，BF∥CE，BF⊥BC，CE=2BF=2AB=4，∠ABF=DCE=120°，G是AF中点．
    （1）求证：AF∥平面DCE；
    （2）求证：BG⊥DF；
    （3）若二面角E-DF-A的大小为150°，求线段DF的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．每逢节假日，在微信好友群发红包逐渐成为一种时尚．某女士每月发红包的个数y（个）与月收入x（千元）具有线性相关关系，用最小二乘法建立回归方程为$\hat y$=8.9x+0.3，则下列说法不正确的是（　　）
    A．y与x具有正线性相关关系
    B．回归直线必过点（$\overline{x}$，$\overline{y}$）
    C．该女士月收入增加1000元，则其发红包的数量约增加9个
    D．该女士月收入为3000元，则可断定其发红包的数量为27个

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数y=f（x）的图象如图所示，求：
    （1）函数y=f（x）的定义域；
    （2）函数y=f（x）的值域．

    查看答案和解析>>

    同步练习册答案