
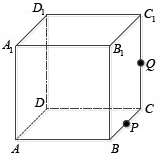
 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是①③④⑤(写出所有正确命题的编号).
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是①③④⑤(写出所有正确命题的编号).分析 过点A,P,Q的平面必与面ADA1,BC1C相交,且交线平行,据此,当Q为C1C中点时,截面与面ADD1交与AD1,为等腰梯形,据此可以对①③进行判断;
连接AP,延长交DC于一点M,再连接MQ并延长其交D1D于N,连接AN,可见,截面此时不会与面ABB1相交,据此判断②;
当CQ=1时,截面为底为$\sqrt{2}$,腰长为$\frac{\sqrt{5}}{2}$的等腰梯形,由此可求其面积,判断④;由$CQ=\frac{3}{4}$作出满足条件的图形,由线面位置关系找出截面,进一步求得C1R判断⑤.
解答 解:连接AP并延长交DC于M,再连接MQ.
当0<CQ<$\frac{1}{2}$时,MQ的延长线交线段D1D与点N,且N在D1与D之间,连接AN,则截面为四边形APQN;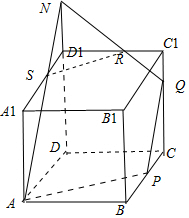
特别的当Q为中点即CQ=$\frac{1}{2}$时,N点与D1重合,此时截面四边形APQN为等腰梯形,故①,③正确;
当$\frac{3}{4}$<CQ<1时,MQ与DD1延长线相交于一点N,再连接AN,与A1D1交于一点,此时截面是五边形,故②错误;
当CQ=1时,MQ交DD1延长线于N点,且DD1=D1N=1,连接AN交A1D1于的中点位置,此时,截面四边形是边长为$\frac{\sqrt{5}}{2}$的菱形,其对角线长为正方体的对角线长$\sqrt{3}$,另一条对角线长为面对角线长为$\sqrt{2}$,所以s=$\frac{1}{2}$×$\sqrt{2}$×$\sqrt{3}$=$\frac{\sqrt{6}}{2}$,故④正确;
当CQ=$\frac{3}{4}$时,如图,延长DD1至N,使D1N=$\frac{1}{2}$,连接AN交A1D1于S,连接NQ交C1D1于R,连接SR,
可证AN∥PQ,由△NRD1∽△QRC1,可得C1R:D1R=C1Q:D1N=1:2,故可得C1R=$\frac{1}{3}$,故⑤正确.
∴正确命题的序号是①③④⑤.
故答案为:①③④⑤.
点评 本题考查命题的真假判断与应用,考查了截面的性质,关键是利用面面平行、面面相交的性质确定截面的顶点,是中档题.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:高中数学 来源: 题型:选择题
| A. | 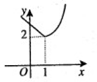 | B. |  | C. | 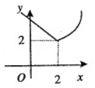 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -15 | B. | -3 | C. | 3 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=1+$\frac{x-|x|}{4}$.
已知函数f(x)=1+$\frac{x-|x|}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com