
科目:高中数学 来源: 题型:解答题
| 参加纪念活动的环节数 | 0 | 1 | 2 | 3 |
| 概率 | $\frac{1}{6}$ | m | n | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{π}$ | B. | $\frac{{3\sqrt{3}}}{4π}$ | C. | $\frac{{\sqrt{3}}}{4π}$ | D. | $\frac{{2\sqrt{3}}}{3π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
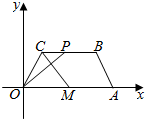 在平面直角坐标系xOy中,已知四边形OABC是等腰梯形,OA∥BC,$A(6,0),C(1,\sqrt{3})$,点M满足$\overrightarrow{OM}=\frac{1}{2}\overrightarrow{OA}$,点P在线段BC上运动(包括端点),如图.
在平面直角坐标系xOy中,已知四边形OABC是等腰梯形,OA∥BC,$A(6,0),C(1,\sqrt{3})$,点M满足$\overrightarrow{OM}=\frac{1}{2}\overrightarrow{OA}$,点P在线段BC上运动(包括端点),如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{2}{21}$ | C. | $\frac{1}{18}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
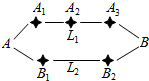 “十一黄金周”期间某市再次迎来了客流高峰,小李从该市的A地到B地有L1、L2两条路线(如图),L1路线上有A1、A2、A3三个路口,各路口遇到堵塞的概率均为$\frac{2}{3}$;L2路线上有B1、B2两个路口,各路口遇到堵塞的概率依次为$\frac{3}{4}$、$\frac{3}{5}$.
“十一黄金周”期间某市再次迎来了客流高峰,小李从该市的A地到B地有L1、L2两条路线(如图),L1路线上有A1、A2、A3三个路口,各路口遇到堵塞的概率均为$\frac{2}{3}$;L2路线上有B1、B2两个路口,各路口遇到堵塞的概率依次为$\frac{3}{4}$、$\frac{3}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com