
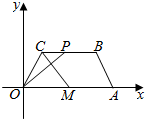
 在平面直角坐标系xOy中,已知四边形OABC是等腰梯形,OA∥BC,$A(6,0),C(1,\sqrt{3})$,点M满足$\overrightarrow{OM}=\frac{1}{2}\overrightarrow{OA}$,点P在线段BC上运动(包括端点),如图.
在平面直角坐标系xOy中,已知四边形OABC是等腰梯形,OA∥BC,$A(6,0),C(1,\sqrt{3})$,点M满足$\overrightarrow{OM}=\frac{1}{2}\overrightarrow{OA}$,点P在线段BC上运动(包括端点),如图.分析 (Ⅰ)由已知点的坐标求出向量的坐标,然后利用数量积求夹角公式得答案;
(Ⅱ)设出P的坐标$P(t,\sqrt{3})$,由$({\overrightarrow{OA}+λ\overrightarrow{OP}})⊥\overrightarrow{CM}$,可得其数量积为0,转化为λ关于t的函数式求解.
解答 解:(Ⅰ)由题意可得$\overrightarrow{OA}=(6,0),\overrightarrow{OC}=(1,\sqrt{3})$,$\overrightarrow{OM}=\frac{1}{2}\overrightarrow{OA}=(3,0)$,
$\overrightarrow{CM}=(2,-\sqrt{3}),\overrightarrow{CO}=(-1,-\sqrt{3})$,
故$cos∠OCM=cos<\overrightarrow{CO},\overrightarrow{CM}>$=$\frac{\overrightarrow{CO}•\overrightarrow{CM}}{|\overrightarrow{CO}||\overrightarrow{CM}|}=\frac{\sqrt{7}}{14}$;
(Ⅱ)设$P(t,\sqrt{3})$,其中1≤t≤5,
$λ\overrightarrow{OP}=(λt,\sqrt{3}λ)$,$\overrightarrow{OA}-λ\overrightarrow{OP}=(6-λt,-\sqrt{3}λ)$,$\overrightarrow{CM}=(2,-\sqrt{3})$,
若$({\overrightarrow{OA}+λ\overrightarrow{OP}})⊥\overrightarrow{CM}$,则$(\overrightarrow{OA}+λ\overrightarrow{OP})•\overrightarrow{CM}=0$,即12-2λt+3λ=0,
可得(2t-3)λ=12.
若t=$\frac{3}{2}$,则λ不存在;
若t$≠\frac{3}{2}$,则$λ=\frac{12}{2t-3}$,
∵t∈[1,$\frac{3}{2}$)∪($\frac{3}{2},5$],
∴λ∈(-∞,-12]∪[$\frac{12}{7},+∞$).
∴实数λ的取值范围是(-∞,-12]∪[$\frac{12}{7},+∞$).
点评 本题考查平面向量数量积运算,考查了由数量积求斜率的夹角,训练了函数值域的求法,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小正周期为$\frac{π}{2}$的奇函数 | B. | 最小正周期为π的奇函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的偶函数 | D. | 最小正周期为π的偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对于函数f:A→B,其值域是集合B | |
| B. | 函数y=1与y=x0是同一个函数 | |
| C. | 两个函数的定义域、对应关系相同,则表示同一个函数 | |
| D. | 映射是特殊的函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com