练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知点P(2，－1)．

    (1)求过点P且与原点距离为2的直线l的方程；

    (2)求过点P且与原点距离最大的直线l的方程，最大距离是多少？


    解析：(1)①当l的斜率k不存在时显然成立，此时l的方程为x＝2.

    ②当l的斜率k存在时，

    设l：y＋1＝k(x－2)，即kx－y－2k－1＝0，

    由点到直线的距离公式得＝2，解得k＝，

    所以l：3x－4y－10＝0.

    故所求l的方程为x＝2或3x－4y－10＝0.

    (2)数形结合可得，过点P且与原点O距离最大的直线是过点P且与PO垂直的直线．

    由l⊥OP，得klkOP＝－1，所以kl＝－＝2.

    由直线方程的点斜式得直线l的方程为y＋1＝2(x－2)，

    即2x－y－5＝0，

    即直线2x－y－5＝0是过点P且与原点O距离最大的直线，最大距离为＝.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知函数f(x)＝2x满足f(m)·f(n)＝2，则mn的最大值为(　　)

    A.　        B.         C.          D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在数列{an},{bn}中,a1=2,b1=4,且an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列(n∈N*).

    (1) 求a2,a3,a4及b2,b3,b4,由此猜测{an},{bn}的通项公式,并证明你的结论;

    (2) 求证:++…+<.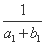

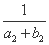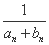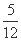    查看答案和解析>>

    科目：高中数学 来源： 题型：


    两条平行直线4x－3y＋m＝0和8x－6y＋n＝0间的距离是(　　)

    A.                 B．|m－n|

    C.                D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    △ABC的两点A，B在直线l1：2x－y＋3＝0上，点C在直线l2：2x－y－1＝0上，若△ABC的面积为2，则AB边的长为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，过抛物线y2＝2px(p>0)的焦点F的直线l交抛物线于点A、B，交其准线于点C，若|BC|＝2|BF|，且|AF|＝3，则此抛物线方程为(　　)

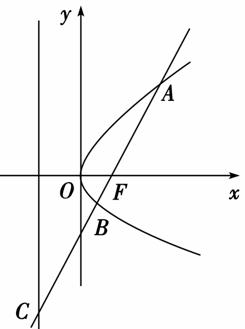
    A．y2＝9x               B．y2＝6x

    C．y2＝3x               D．y2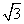＝x

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知动圆C经过点(0,1)，且在x轴截得的弦长为2，记该圆圆心的轨迹为E.

    (1)求曲线E的方程；

    (2)过点M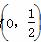的直线m交曲线E于A，B两点，过A，B两点分别作曲线E的切线，两切线交于点C，当△ABC的面积为2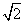时，求直线m的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    双曲线x2－my2＝1的实轴长是虚轴长的2倍，则m等于(　　)

    A．1       B．2       C．3        D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    P为抛物线4x上任意一点，P在y轴上的射影为Q，点M(4,5)，则PQ与PM长度之和的最小值为(　　)

    A.＋2              B.＋1    C.－1              D.

    查看答案和解析>>

    同步练习册答案