
在数列{an},{bn}中,a1=2,b1=4,且an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列(n∈N*).
(1) 求a2,a3,a4及b2,b3,b4,由此猜测{an},{bn}的通项公式,并证明你的结论;
(2) 求证: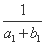 +
+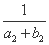 +…+
+…+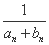 <
<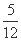 .
.
(1) 由题意得2bn=an+an+1,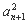 =bnbn+1,由此可得
=bnbn+1,由此可得
a2=6,b2=9,a3=12,b3=16,a4=20,b4=25.
猜测an=n(n+1),bn=(n+1)2.
用数学归纳法证明:
①当n=1时,由已知可得结论成立.
②假设当n=k时结论成立,即
ak=k(k+1),bk=(k+1)2.
那么当n=k+1时,
ak+1=2bk-ak=2(k+1)2-k(k+1)=(k+1)(k+2),
bk+1=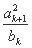 =(k+2)2.
=(k+2)2.
所以当n=k+1时,结论也成立.
由①②可知an=n(n+1),bn=(n+1)2对一切正整数都成立.
(2) 当n=1时,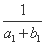 =
=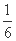 <
<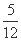 .
.
当n≥2时,由(1)知an+bn=(n+1)(2n+1)>2(n+1)n.
故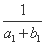 +
+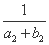 +…+
+…+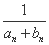
<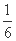 +
+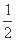 ×
×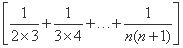
=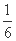 +
+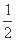 ×
×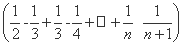
=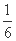 +
+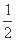 ×
×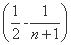 <
<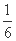 +
+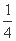 =
=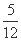 ,
,
综上,原不等式成立.


科目:高中数学 来源: 题型:
在古希腊毕达哥拉斯学派把1,3,6,10,15,21,28,…,这些数叫做三角形数,因为这些数对应的点可以排成一个正三角形,如下图,
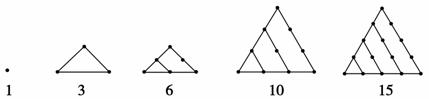
则第n个三角形数为( )
A.n B.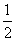 n(n+1) C.n2-1 D.
n(n+1) C.n2-1 D.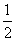 n(n-1)
n(n-1)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点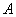 (0,-2),椭圆
(0,-2),椭圆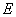 :
: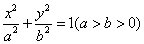 的离心率为
的离心率为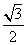 ,
,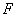 是椭圆的焦点,直线
是椭圆的焦点,直线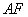 的斜率为
的斜率为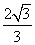 ,
,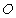 为坐标原点.
为坐标原点.
(1) 求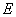 的方程;
的方程;
(2) 设过点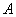 的直线
的直线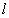 与
与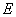 相交于
相交于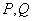 两点,当
两点,当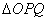 的面积最大时,求
的面积最大时,求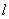 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
以两点A(-3,-1)和B(5,5)为直径端点的圆的方程是( )
A.(x-1)2+(y+2)2=100 B.(x-1)2+(y-2)2=100
B.(x-1)2+(y-2)2=100
C.(x-1)2+(y-2)2=25 D.(x+1)2+(y+2)2=25
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com