练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在古希腊毕达哥拉斯学派把1,3,6,10,15,21,28，…，这些数叫做三角形数，因为这些数对应的点可以排成一个正三角形，如下图，

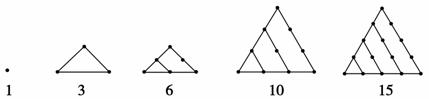
    则第n个三角形数为(　　)

    A．n                   B.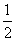n(n＋1)    C．n2－1                D.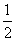n(n－1)


    B


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    函数的定义域为________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝ax＋2a＋1，当x∈[－1,1]时，f(x)有正值也有负值，则实数a的取值范围为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a<0，－1<b<0，那么下列不等式成立的是(　　)

    A．a>ab>ab2            B．ab2>ab>a

    C．ab>a>ab2            D．ab>ab2>a

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若x>y，a>b，则在①a－x>b－y，②a＋x>b＋y，③ax>by，④x－b>y－a，⑤>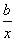这五个式子中，恒成立的所有不等式的序号是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    无限循环小数可以化为有理数，如，…，请你归纳出0.0＝__________________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设f(x)＝，先分别求f(0)＋f(1)，f(－1)＋f(2)，f(－2)＋f(3)，然后归纳猜想一般性结论，并给出证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝2x满足f(m)·f(n)＝2，则mn的最大值为(　　)

    A.　        B.         C.          D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在数列{an},{bn}中,a1=2,b1=4,且an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列(n∈N*).

    (1) 求a2,a3,a4及b2,b3,b4,由此猜测{an},{bn}的通项公式,并证明你的结论;

    (2) 求证:++…+<.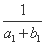

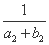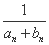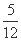    查看答案和解析>>

    同步练习册答案