
| A. | 4033 | B. | -4033 | C. | 4034 | D. | -4034 |
分析 利用题意首先求解f(x)+f(2-x)的值,然后利用倒序相加求和的方法即可求得最终结果.
解答 解:结合函数的解析式可得:
f(x)+f(2-x)=x+sinπx+(2-x)+sinπ(2-x)=x+sinπx+(2-x)-sinπx=2.
设 $S=f(\frac{1}{2017})+f(\frac{2}{2017})+f(\frac{3}{2017})+…+f(\frac{4033}{2017})$,①
则:$S=f(\frac{4033}{2017})+f(\frac{4032}{2017})+f(\frac{4031}{2017})+…+f(\frac{1}{2017})$,②
①+②可得:$2S=[f(\frac{1}{2017})+f(\frac{4033}{2017})]+…+[f(\frac{4033}{2017})+f(\frac{1}{2017})]$,
即 2S=2+2+…+2=2×4033,∴S=4033,
据此可得:$f(\frac{1}{2017})+f(\frac{2}{2017})+f(\frac{3}{2017})+…+f(\frac{4033}{2017})=4033$.
故选:A.
点评 本题考查函数值的求解,倒序相加求和,诱导公式及其应用等,重点考查学生对基础概念的理解和计算能力,属于中等题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
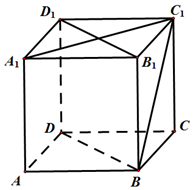 如图,已知正方体ABCD-A${\;}_{{1}_{\;}}$B1C1D1,BD,BC1,B1D1,A1C1分别为各个面的对角线;
如图,已知正方体ABCD-A${\;}_{{1}_{\;}}$B1C1D1,BD,BC1,B1D1,A1C1分别为各个面的对角线;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=x+\frac{4}{x},(x≠0)$ | B. | y=-x2+2x+3 | ||
| C. | $y=sinx+\frac{4}{sinx}(0<x<π)$ | D. | y=ex+4e-x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b⇒ac2>bc2 | B. | a<b<0⇒a2b>b3 | ||
| C. | $\frac{a}{b}$>1⇒a>b且b>0 | D. | a3>b3,ab>0⇒$\frac{1}{a}$<$\frac{1}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)图象关于点P(1,0)对称 | B. | f(x)图象关于直线x=1对称 | ||
| C. | f(x)在[0,1]上是减函数 | D. | f(2)=f(0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com