【题目】已知直线
，抛物线C：
上一动点P到直线
和
轴距离之和的最小值是（ ）
A.1B.2C.
D.
【答案】A
【解析】
抛物线
上一动点P到直线
和
轴距离之和最小转化为：抛物线上一动点P到直线和直线x＝-1的距离之和最小，x＝1是抛物线的准线，则P到x＝1的距离等于PF，F（1，0）为抛物线的焦点，过F作
垂线，和抛物线的交点就是P，所以点P到直线
的距离和到轴的距离之和的最小值就是F（1，0）到直线距离再减1．
解：x＝1是抛物线的准线，抛物线的焦点F（1，0），
则P到x＝1的距离等于PF，
过F作垂线，和抛物线的交点就是P，
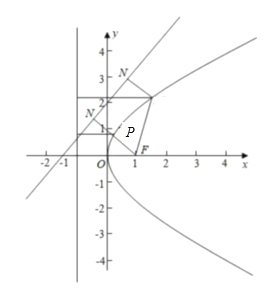
所以点P到直线：的距离和到直线：x＝1的距离之和的最小值
就是F（1，0）到直线距离，
所以最小值
．
抛物线上一动点P到直线和轴的距离之和的最小值是：21＝1
故选：A．
小题狂做系列答案科目：高中数学 来源： 题型：
【题目】平面直角坐标系中，
为坐标原点，射线
与
轴正半轴重合，射线
在第一象限，且与轴正半轴的夹角为
，在上有点列
，在上有点
，已知
，
（1）求点
和
的坐标；
（2）求
的坐标；
（3）求
面积的最大值，并求出此时的
值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆C：
，直线1过原点O．
（1）若直线l与圆C相切，求直线l的斜率；
（2）若直线l与圆C交于A、B两点，点P的坐标为
，若
．求直线l的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某工厂去年某产品的年产量为100万只，每只产品的销售价为10元，固定成本为8元
今年，工厂第一次投入100万元
科技成本
，并计划以后每年比上一年多投入100万元科技成本，预计产量年递增10万只，第
次投入后，每只产品的固定成本为
为常数，
且
，若产品销售价保持不变，第次投入后的年利润为
万元．
（1）求
的值，并求出的表达式；
（2）问从今年算起第几年利润最高？最高利润为多少万元？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列命题正确的是
（1）命题“
，
”的否定是“
，
”；
（2）l为直线，
，
为两个不同的平面，若
，
，则
；
（3）给定命题p，q，若“
为真命题”，则
是假命题；
（4）“
”是“
”的充分不必要条件．
A. （1）（4）B. （2）（3）C. （3）（4）D. （1）（3）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
