
| A�� | $��{0��\frac{{\sqrt{3}}}{3}}��$ | B�� | ��-1��0] | C�� | $��{-1��\frac{{\sqrt{3}}}{3}}��$ | D�� | $��{-1��0}���ȣ�{0��\frac{{\sqrt{3}}}{3}}��$ |
���� ���÷ֶκ����������֪�������г�����ʽ�飬ת����⼴�ɣ�
��� �⣺�����⣬��$\left\{\begin{array}{l}{log_{\frac{1}{3}}}x��\frac{1}{2}\\ x��0\end{array}\right.$��$\left\{\begin{array}{l}{2^x}��\frac{1}{2}\\ x��0\end{array}\right.$�����$0��a��\frac{{\sqrt{3}}}{3}$��-1��a��0��
��ʵ��a��ȡֵ��ΧΪ$��{-1��\frac{{\sqrt{3}}}{3}}��$��
��ѡC��
���� ���⿼��ֶκ�����Ӧ�ã�����ʽ�����⣬�������������


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [k��-$\frac{11��}{24}$��k��+$\frac{��}{24}$]��k��Z�� | B�� | $[k��+\frac{3��}{8}��k��+\frac{7��}{8}]��k��Z��$ | ||
| C�� | $[2k��-\frac{��}{4}��2k��+\frac{3��}{4}]��k��Z��$ | D�� | $[2k��+\frac{3��}{4}��2k��+\frac{7��}{4}]��k��Z��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-3��3] | B�� | [-1��2] | C�� | [-3��2] | D�� | ��-1��2] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=��x | B�� | y=��2x | C�� | y=��$\sqrt{3}$x | D�� | y=��$\sqrt{2}$x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 1+i | C�� | -1+i | D�� | 1-i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
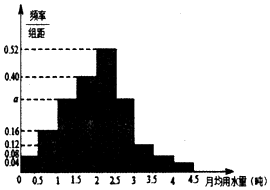 ˮ�ǵ����ϱ������Դ�����ڼ۸�Ƚϱ����ںܶȱˮ�ij��о������Ƶ�ʹ��ˮ��Դ������ص���Դ�˷ѣ�ij������Ϊ���ᳫ��̼����������������������Լ��ˮ���ƻ���������������ˮ�շѷ�������ȷ��һ������������ˮ����x���֣���һλ���������ˮ��������x�IJ��ְ�ƽ���շѣ�����x�IJ��ְ�����շѣ�Ϊ���˽������ˮ�����ͨ�������������ij��100λ����ÿ�˵��¾���ˮ������λ���֣��������ݰ���[0��0.5����[0.5��1����[1��1.5��������[4��4.5���ֳ�9�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
ˮ�ǵ����ϱ������Դ�����ڼ۸�Ƚϱ����ںܶȱˮ�ij��о������Ƶ�ʹ��ˮ��Դ������ص���Դ�˷ѣ�ij������Ϊ���ᳫ��̼����������������������Լ��ˮ���ƻ���������������ˮ�շѷ�������ȷ��һ������������ˮ����x���֣���һλ���������ˮ��������x�IJ��ְ�ƽ���շѣ�����x�IJ��ְ�����շѣ�Ϊ���˽������ˮ�����ͨ�������������ij��100λ����ÿ�˵��¾���ˮ������λ���֣��������ݰ���[0��0.5����[0.5��1����[1��1.5��������[4��4.5���ֳ�9�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��+�ޣ� | B�� | ��1��3�� | C�� | ��0��1���ȣ�1��3�� | D�� | $[\frac{3}{2}��3��$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com