
| A. | [kπ-$\frac{11π}{24}$,kπ+$\frac{π}{24}$](k∈Z) | B. | $[kπ+\frac{3π}{8},kπ+\frac{7π}{8}](k∈Z)$ | ||
| C. | $[2kπ-\frac{π}{4},2kπ+\frac{3π}{4}](k∈Z)$ | D. | $[2kπ+\frac{3π}{4},2kπ+\frac{7π}{4}](k∈Z)$ |
分析 利用函数y=Asin(ωx+φ)的图象和性质,函数y=Asin(ωx+φ)的图象变换规律,求得$f(x+\frac{π}{12})+f(x-\frac{π}{6})$的单调递增区间.
解答 解:∵函数$f(x)=sin(ωx+φ)(ω>0,|φ|<\frac{π}{2})$的最小正周期为$\frac{2π}{ω}$=π,∴ω=2.
f(x)的图象向左平移$\frac{π}{3}$个单位后,得到y=sin[2(x+$\frac{π}{3}$)+φ]=sin(2x+$\frac{2π}{3}$+φ)的图象,
根据所得图象关于直线x=0对称,可得函数y=sin(2x+$\frac{2π}{3}$+φ)为偶函数,∴$\frac{2π}{3}$+φ=kπ+$\frac{π}{2}$,k∈Z,
故φ=-$\frac{π}{6}$,所得函数的解析式为y=sin(2x+$\frac{2π}{3}$-$\frac{π}{6}$)=cos2x.
则$f(x+\frac{π}{12})+f(x-\frac{π}{6})$=cos2(x+$\frac{π}{12}$)+cos2(x-$\frac{π}{6}$)=cos(2x+$\frac{π}{6}$)+cos(2x-$\frac{π}{3}$)
=cos(2x+$\frac{π}{6}$)+sin[(2x-$\frac{π}{3}$)+$\frac{π}{2}$]=cos(2x+$\frac{π}{6}$)+sin(2x+$\frac{π}{6}$)=$\sqrt{2}$sin(2x+$\frac{π}{6}$+$\frac{π}{4}$)=$\sqrt{2}$sin(2x+$\frac{5π}{12}$).
令2kπ-$\frac{π}{2}$≤2x+$\frac{5π}{12}$≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{11π}{24}$≤x≤kπ+$\frac{π}{24}$,故函数的单调递增区间为[kπ-$\frac{11π}{24}$,kπ+$\frac{π}{24}$],
故选:A.
点评 本题主要考查函数y=Asin(ωx+φ)的图象和性质,函数y=Asin(ωx+φ)的图象变换规律,属于中档题.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{5}$ | B. | $±\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $±\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
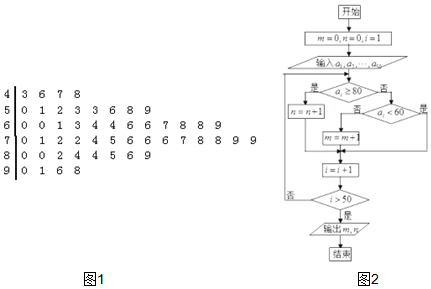
| A. | m=26,n=12 | B. | m=38,n=12 | C. | m=12,n=12 | D. | m=24,n=10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
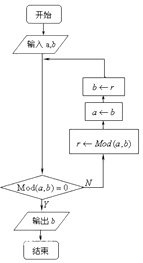 辗转相除法,又名欧几里得算法,乃求两个正整数之最大公因子的算法.它是已知最古老的算法,在中国则可以追溯至东汉出现的《九章算术》,图中的程序框图所表述的算法就是欧几里得辗转相除法,若输入a=5280,b=12155,则输出的b=55.
辗转相除法,又名欧几里得算法,乃求两个正整数之最大公因子的算法.它是已知最古老的算法,在中国则可以追溯至东汉出现的《九章算术》,图中的程序框图所表述的算法就是欧几里得辗转相除法,若输入a=5280,b=12155,则输出的b=55.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{{\sqrt{3}}}{3}})$ | B. | (-1,0] | C. | $({-1,\frac{{\sqrt{3}}}{3}})$ | D. | $({-1,0})∪({0,\frac{{\sqrt{3}}}{3}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com