
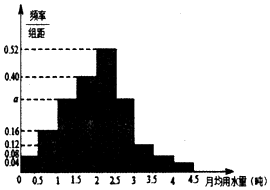
 ˮ�ǵ����ϱ������Դ�����ڼ۸�Ƚϱ����ںܶȱˮ�ij��о������Ƶ�ʹ��ˮ��Դ������ص���Դ�˷ѣ�ij������Ϊ���ᳫ��̼����������������������Լ��ˮ���ƻ���������������ˮ�շѷ�������ȷ��һ������������ˮ����x���֣���һλ���������ˮ��������x�IJ��ְ�ƽ���շѣ�����x�IJ��ְ�����շѣ�Ϊ���˽������ˮ�����ͨ�������������ij��100λ����ÿ�˵��¾���ˮ������λ���֣��������ݰ���[0��0.5����[0.5��1����[1��1.5��������[4��4.5���ֳ�9�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
ˮ�ǵ����ϱ������Դ�����ڼ۸�Ƚϱ����ںܶȱˮ�ij��о������Ƶ�ʹ��ˮ��Դ������ص���Դ�˷ѣ�ij������Ϊ���ᳫ��̼����������������������Լ��ˮ���ƻ���������������ˮ�շѷ�������ȷ��һ������������ˮ����x���֣���һλ���������ˮ��������x�IJ��ְ�ƽ���շѣ�����x�IJ��ְ�����շѣ�Ϊ���˽������ˮ�����ͨ�������������ij��100λ����ÿ�˵��¾���ˮ������λ���֣��������ݰ���[0��0.5����[0.5��1����[1��1.5��������[4��4.5���ֳ�9�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ������ ��1����ͼ��������3��������ռ�ٷֱ�Ϊ0.5����0.12+0.08+0.04��=12%��������ɵó���
��2���ɸ���ͳ�����֪ʶ������Ƶ��֮�͵�ֵΪ1��Ƶ��=$\frac{Ƶ��}{���}�����$���ɵ�0.5����0.08+0.16+0.4+0.52+0.12+0.08+0.04+2a��=1����a���������֪�������Z��ȡֵΪ0��2��4������������������¼��ĸ��ʼ��㹫ʽ���ɵó���
��� �⣺��1����ͼ��������3��������ռ�ٷֱ�Ϊ0.5����0.12+0.08+0.04��=12%��
���Լ���ȫ�е�����Ϊx�����ˣ�������0.12x=3.6�����x=30��
���Թ���ȫ������Ϊ30��
��2���ɸ���ͳ�����֪ʶ������Ƶ��֮�͵�ֵΪ1��
��ΪƵ��=$\frac{Ƶ��}{���}�����$��
����0.5����0.08+0.16+0.4+0.52+0.12+0.08+0.04+2a��=1����a=0.3��
��ˮ����[1��1.5]֮��Ļ���Ϊ100��0.3��0.5=15����
����ˮ����[1.5��2]��֮��Ļ���Ϊ100��0.4��0.5=20����
���ݷֲ�����ķ������ܹ���Ҫ��ȡ7������
������ˮ����[1��1.5]֮��Ӧ��ȡ�Ļ���Ϊ$15��\frac{7}{35}=3$����
����ˮ����[1.5��2]��֮��Ļ���Ϊ$20��\frac{7}{35}=4$����
�������֪�������Z��ȡֵΪ0��2��4.$P��X=0��=P��X=2��Y=2��=\frac{C_3^2C_4^2}{C_7^3}=\frac{18}{35}$��$P��X=2��=P��X=1��Y=3��+P��X=3��Y=1��=\frac{C_3^1C_4^3+C_3^3C_4^1}{C_7^3}=\frac{16}{35}$��$P��Z=4��=P��X=0��Y=4��=\frac{C_3^0C_4^4}{C_7^3}=\frac{1}{35}$��
��ֲ���Ϊ��
| Z | 0 | 2 | 4 |
| P | $\frac{18}{35}$ | $\frac{16}{35}$ | $\frac{1}{35}$ |
���� ���⿼����������������¼��ĸ��ʼ��㹫ʽ������ѧ�������㹫ʽ��Ƶ�ʷֲ�ֱ��ͼ�����ʼ���Ӧ�ã�������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��{0��\frac{{\sqrt{3}}}{3}}��$ | B�� | ��-1��0] | C�� | $��{-1��\frac{{\sqrt{3}}}{3}}��$ | D�� | $��{-1��0}���ȣ�{0��\frac{{\sqrt{3}}}{3}}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $4+2\sqrt{2}$ | B�� | $4\sqrt{2}$ | C�� | $3+2\sqrt{2}$ | D�� | $3+\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
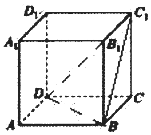 ��������ABCD-A1B1C1D1�У�����A��ƽ���ƽ��ƽ��BDC1��ƽ�����ƽ��A1ADD1����ֱ��m��ƽ�����ƽ��A1ABB1����ֱ��n����ֱ��m��ֱ��n���ɵĽ�Ϊ��������
��������ABCD-A1B1C1D1�У�����A��ƽ���ƽ��ƽ��BDC1��ƽ�����ƽ��A1ADD1����ֱ��m��ƽ�����ƽ��A1ABB1����ֱ��n����ֱ��m��ֱ��n���ɵĽ�Ϊ��������| A�� | $\frac{��}{6}$ | B�� | $\frac{��}{4}$ | C�� | $\frac{��}{3}$ | D�� | $\frac{��}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com