
分析 (1)用极坐标公式,即可把曲线C2的极坐标方程化为普通方程;
(2)把曲线C1的参数方程化为普通方程,利用直线与抛物线C2的方程,
求出直线与抛物线没有交点.
解答 解:(1)将曲线C2的极坐标方程$ρsin(θ-\frac{π}{4})=\sqrt{2}$展开,
得:ρsinθ-ρcosθ=2,
化为普通方程是:y-x=2;①
(2)将C1的参数方程$\left\{\begin{array}{l}{x=1+cos2α}\\{y=\frac{1}{2}cosα}\end{array}\right.$,
∵x=1+2cos2α-1=2cos2α,
y2=$\frac{1}{4}$cos2α,
∴8y2=2cos2α,
化为普通方程是:
y2=$\frac{1}{8}$x②;
所以直线经过该抛物线的焦点F($\frac{1}{32}$,0);
由①、②联立,消去x得:
y2-$\frac{1}{8}$y+$\frac{1}{4}$=0;
∴△=${(\frac{1}{8})}^{2}$-4×$\frac{1}{4}$=-$\frac{63}{64}$<0,
∴c1与c2不会交于两点.
点评 本题考查了直线与抛物线的应用问题,也考查了参数方程与极坐标的应用问题,是综合题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{{5\sqrt{3}}}{3}$ | D. | $\frac{{3\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
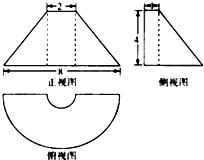 如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )
如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )| A. | 12π | B. | 16π | C. | 20π | D. | 24π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 1-$\frac{{\sqrt{13}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 根据下列算法语句,将输出的A值依次记为a1,a2,…,an,…,a2015
根据下列算法语句,将输出的A值依次记为a1,a2,…,an,…,a2015查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com